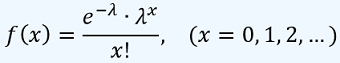
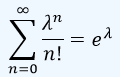

| Menú Probabilidad y Estadística | Distribución Continua Uniforme | Distribución Normal |
DISTRIBUCION DE POISSON p(x;λ). La distribución de POISSON es también un caso particular de probabilidad de variable aleatoria discreta, el cual debe su nombre a Simeón Dennis Poisson (1781-1840), un francés que la desarrolló a partir de los estudios que realizó durante la última etapa de su vida. Esta distribución se utiliza para describir ciertos esperimentos llamados procesos de Poisson. En el tipo de experimentos en que se producen valores de una variable aleatoria discreta X establecida como el número de resultados (individuos, partículas) que ocurren (o llegan) durante (a) un intervalo de tiempo o región específica, son los experimentos de Poisson [Walpole]. En el experimento de Poisson los resultados u ocurrencias son expresados por unidad de área, tiempo, pieza, etc:
Las característica de la distribución de Poisson, son:
- En esta distribución el número de resultados que ocurren por unidad de tiempo o área está dado por el azar.
- El número de resultados que ocurren por unidad de tiempo o área es independiente del número de resultados que ocurren en cualquier otro intervalo dado de tiempo o área del espacio disjunto. Esto implica que el número de
resultados (o individuos, partículas) que se producen (o llegan) durante un intervalo de tiempo es independiente al número correspondiente que ocurrió antes, luego el proceso de
Poisson NO tiene memoria.
- La probabilidad de que ocurra un solo resultado (o llegue un individuo o una partícula) durante un intervalo de tiempo muy corto o en una región pequeña
es proporcional a la longitud del intervalo o al tamaño de la región.
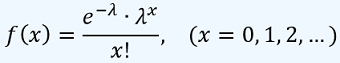
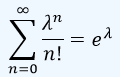
Observe que el parámetro λ nos da el número promedio de resultados que se presentan por unidad de tiempo o área, mientras que la variable aleatoria X es para cualquiera de los valores que se puedan presentar precisamente de este número de resultados por unidad de tiempo o área. Luego la probabilidad de que X tome un valor que esté cercano o igual al promedio λ, debe ser la más alta ya que es lo que ocurre habitualmente, mientras que si se calcula la probabilidad para un número de resultados muy lejano a λ bien por arriba o por abajo, esta probabilidad es muy baja ya que serán resultados atípicos. Así, si se sabe que el promedio de accidentes que ocurren por mes en una autopista es de 20 (λ=20), la probabilidad de que en un mes cualquiera sólo se presenten 5 accidentes, es decir, P(X=5), es muy bajo ya que es algo inusual.
Ejemplo 1. El número de personas que ingresan diariamente a la enfermería de una universidad, tiene una distribución Poisson de media 6. ¿A qué es igual la probabilidad de que,
en un día en particular, el número de personas que ingresan a la enfermería, en dicha universidad, sea menor o igual a 3?
Solución: Sea X = "número de personas que ingresan diariamente a la enfermería". Por los datos del problema, se sabe que X se distribuye
de acuerdo a la Poisson con λ = 6, y se pide P(X ≤ 3), por lo tanto:
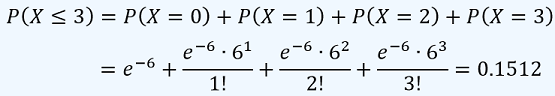
En algunos casos nos dan el promedio en un intervalo o región y se pide calcular un número de resultados en un intervalo o región definidos de forma distinta, es decir, la variable aleatoria X aparentemente estaría definida de forma diferente a la establecida por el promedio (parámetro λ), lo cual No puede ocurrir. En este caso, se debe redefinir el promedio de resultados o parámetro λ de la siguiente forma:
|
Si Xt es la variable aleatoria que denota el número de individuos (partículas) que llegan en el intervalo de tiempo (0, t], entonces, se tiene que por unidad de tiempo o área Xt tiene una distribución de Poisson con parámetro λt (tomado de probabilidad de [Ros]). |
Ejemplo. En el problema anterior, si del miércoles al viernes se va a realizar un evento en la universidad llamado Eliminatorias deportivas interuniversitarias, ¿cuál es la probabilidad de que ingresen 21 personas a la enfermería durante este evento deportivo?
Solución. El intervalo de tiempo del evento deportivo es (0,3] días, luego el parámetro λ se recalcula ahora como 6*3= 18 ingresos a enfermería/evento o 18 ingresos enfermería por periodo de 3 días.
La probabilidad pedida es
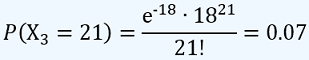
Ahora podríamos pensar, que ingresen 21 personas en los tres días del evento, ¿será lo mismo a que ingresen 7 personas por día y resolver el problema con el mismo parámetro λ de 6 ingresos a enfermería por día?, veamos:
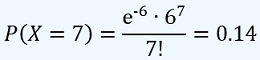
esta probabilidad obtenida es muy diferente. Luego, se debe ajustar el parámetro al nuevo intervalo y No la variable aleatoria.
Las tablas están limitadas para unos valores de la media de ocurrencia de sucesos, λ. Así para el ejemplo, se observa una muestra de una tabla en la siguiente figura:

En la cual se busca en la media o λ = 6 y luego desde allí hacia abajo hasta x=3, con lo cual se tiene la probabilidad P(X ≤ 3) = 0.1512, como se había calculado en el ejemplo.
Al contrario de las las tablas, ya no se tiene la limitación para unos valores de la media de ocurrencia de sucesos, λ. Con nuestra propia calculadora Calculadora Distribución de Poisson, se ingresan los datos en la sección Acumulada, como se observa en la siguiente figura:
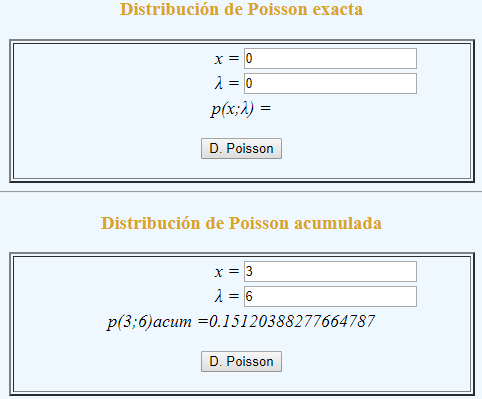 |
La distribución de Poisson se puede considerar como una forma limitante de la binomial cuando n es grande (n → ∞) y p pequeño (p → 0), o en caso de n grande y p cercano a 1 (p → 1), se puede usar la distribución de Poisson para aproximar probabilidades binomiales intercambiando lo que se defina en el problema desde la binomial como éxito o fracaso. De esta forma:
| Sea X una variable aleatoria binomial con distribución de probabilidad b(x;n,p). Cuando (n → ∞), (p → 0) y np → λ permanece constante, entonces |
Ejemplo. Si una vacuna genera una protección 99,98% efectiva contra una enfermedad, ¿cuál es la probabilidad de que se enfermen exactamente 6 individuos de una población de 15.000 personas vacunadas?
Solución. Como la efectividad es del 99,98%, luego el 0,02% de los vacunados contraerían la enfermedad, o p = 0,0002:
λ = np = (15.000)(0,0002)=3; X = 6 ⇒ P(X=6) = (e−3 ∙ 36/6!) = 0,0504
Ahora evalúese con nuestra Simulación Quiz Interactivo de la distribución de Poisson
| Menú Probabilidad y Estadística | Distribución Continua Uniforme | Distribución Normal |