
| Menú Probabilidad y Estadística | Distribución Continua Uniforme | Distribución Normal |
En la distribución binomial se repite un experimento bajo las mismas condiciones n veces y se calcula la probabilidad de obtener de manera
exacta k éxitos. En la binomial el número de repeticiones se fija o permanece constante mientras que el número de éxitos es aleatorio. En la distribución
Binomial Negativa, se enfoca a resolver preguntas como ¿Cuál es la probabilidad de tener que repetir el experimento n veces para obtener el k éxitos?. Es decir,
que en este caso el número de éxitos es el que permanece constante mientras que el número de ensayos X es aleatorio.
Se establece a continuación la funcion de masa de probabilidad (f.m.p.), tenga en cuenta también el rango (es decir, el conjunto de valores x en
que f(x) se define), junto con la fórmula para f(x):
En un departamento de control de calidad se inspeccionan las unidades terminadas que provienen de una línea de producción. Si la proporción de unidades defectuosas es de 0.02, ¿cuál es la probabilidad de que la vigésima unidad inspeccionada sea la tercera que se encuentra defectuosa?
Solución Sea X := "número de unidades que es necesario inspeccionar hasta obtener exactamente tres unidades defectuosas". Es claro que X = b*(X=20,k=3,p=0.02). Por lo tanto,
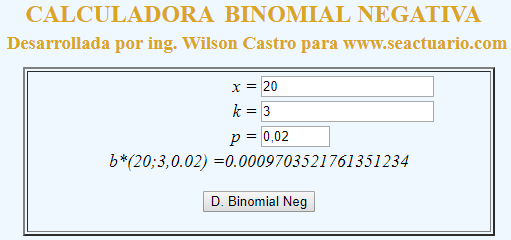
Abra la Calculadora de la Distribución Binomial Negativa de www.seacutario.com, e ingrese los datos correspondientes del problema, como se observa en la siguiente figura:
| Menú Probabilidad y Estadística | Distribución Continua Uniforme | Distribución Normal |