
con n = 1, 2,... y con k = 0, 1,...,n. La interpretación es:

| Menú Probabilidad y Estadística | Distribuciones Discretas | Distribución Continua Uniforme | Cuestionario Distribución Binomial |
Las distribuciones especiales de variables aleatorias discretas que se tratan en este curso, son:
Luego se tratarán las variables aleatorias continuas como la distribución Normal
En las principales distribuciones de probabilidad de variables aleatorias discretas, suele aparecer en la expresión de la función de masa de probabilidad, el número combinatorio nCk, que ya se trabajó en el tema de Conteo, para representar el caso de arreglos en que No importa el orden de los elementos, recordemos:

con n = 1, 2,... y con k = 0, 1,...,n. La interpretación es:
Definición. Un experimento aleatorio, se denomina ensayo de Bernoulli, si se caracteriza por:
Definición. Si X es el número de éxitos en n experimentos de Bernoulli,X es llamada una variable aleatoria binomial, y la forma en que se distribuye esta variable, la distribución binomial.
En la distribución binomial, se establece a continuación la funcion de masa de probabilidad (f.m.p.), tenga en cuenta también el rango (es decir, el conjunto de valores x en que f(x) se define), junto con la fórmula para f(x):
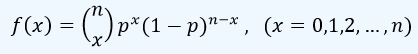
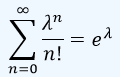
Un estudiante toma un examen de opción múltiple con n: l0 preguntas. No ha asistido a clases ni estudiado para este examen, por lo cual planea adivinar en cada pregunta, marcando en un lápiz con bordes definidos las letras A, B, C y D en cada borde y arrojando el lápiz, con lo que responde de forma aleatoria. (Hay 4 opciones para cada pregunta). Sea X sea la cantidad de preguntas de las 10 que el alumno adivina correctamente. Entonces X es una variable aleatoria binomial, ya que todas las condiciones se cumplen:
La probabilidad de que el estudiante apruebe el examen con 6 aciertos, es
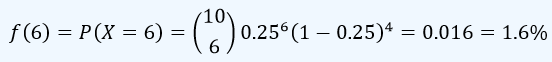
que es una probabilidad baja, no obstante, la probabilidad total de que apruebe el examen es superior, ya que esto lo logra con X=6, o X=7, o X=8 o X=9 o X = 10. Para calcular esto, existen las tablas de la binomial, para el valor exacto que tome X, como en el caso anterior (X=6), o también acumulada,para evaluar por ejemplo P(X ≤ 5). En la tabla acumulada, se tiene un encabezado para tabular de acuerdo al valor de la probabilidad de éxito p, y a los lados se tienen los valores de n y para cada uno de estos los valores del número de éxitos o x, como se observa en la siguiente muestra de esta tabla:
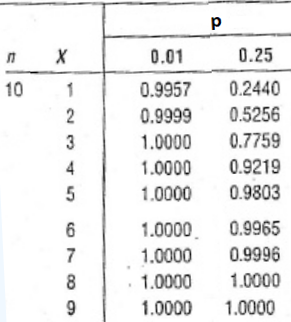
Para evaluar la probabilidad total de aprobar el examen, se requiere el análisis y los valores de la tabla acumulada de la binomial, según:

Existen muchas aplicaciones y software para el manejo de los datos en las diferentes distribuciones de probabilidad. Desde las hojas de cálculo como Excel, a programas específicos como R, Geogebra, Matlab, etc, etc.
Se ilustrará aquí el uso de nuestro propio programa; Calculadora de la D. Binomial
La calculadora tiene 4 secciones, como se observa en la figura:

En la primera sección, se evalúa el factorial de un número, en la segunda sección el número combinatorio, y en las secciones 3 y 4 propiamente la binomial, el binomial exacto es decir para una cantidad específica de éxitos, y la binomial acumulada.
Para el ejemplo, primero se evalúa la probabilidad de que el estudiante apruebe el examen con exactamente 6 aciertos. Ingrese en la sección 3 de la calculadora los datos y luego presiones el botón para evaluar, como se observa en la sig. figura:
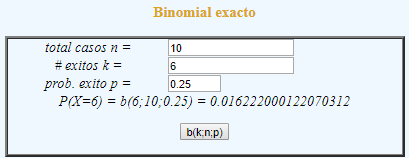
Para la probabilidad total de que apruebe el examen, se ingresan los datos en la siguiente sección, primero para k=10 éxitos que da una probabilidad de 1.0, luego para k=5, como se muestra en la siguiente figura:
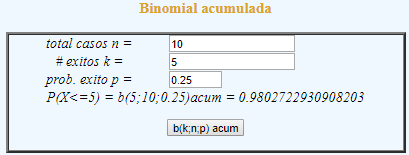
Por útimo, la probabilidad de aprobar el examen será la diferencia entre las dos probabilidades previamente calculadas, como se realizó en el ejemplo.
Ahora practique los conceptos con el Cuestionario Interactivo y Simulado de la Distribución Binomial
| Menú Probabilidad y Estadística | Distribuciones Discretas | Distribución Continua Uniforme | Cuestionario Distribución Binomial |