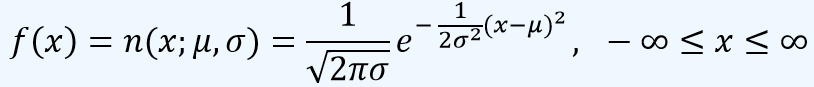
Donde π = 3.14159... y e = 2.71828 ...

| Menú Probabilidad y Estadística | D. Poisson | Tema Siguiente | D. Continua Uniforme |
La distribución de probabilidad de la variable aleatoria Normal X, dada por:
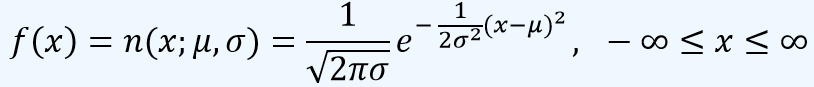

En las distribuciones continuas de probabilidad, para hallar la probabilidad de que la variable aleatoria X tome valores entre x1 y x2, se debe establecer como la integral entre estos valores de la función de densidad de probabilidad. De esta forma el área sombreada en la curva normal de la siguiente figura:

corresponde a la probabilidad:
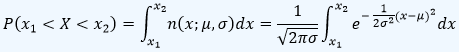
Desarrollar esta integral para realizar el cálculo de probabilidades en una distribución normal, resulta laborioso. Además de acuerdo a los valores de μ y σ se tiene una forma específica de la curva normal o Campana de Gauss. Para tabular estas probabilidades, es posible realizar una transformación de cualquier variable aleatoria normal X en otra variable normal indicada Z con μ = 0 y σ = 1 la cual es la llamada Distribución Normal Estandar n(z;0,1), con la variable aleatoria Z de acuerdo con:
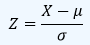
Definición. La distribución de una variable aleatoria normal con media μ = 0 y Desviación estándar σ = 1, es la Distribución Normal Estandar n(z;0,1)
Todas las tablas de la dstribución normal, son realmente de la Distribución Normal Estandar n(z;0,1).
Se encuentran las tablas de la distribución normal estándar, en algunos casos solamente para los valores de z positivos ya que por simetría se pueden deducir los correspondientes del lado izquierdo o valores negativos. Se muestra una tabla típica con valores negativos y positivos, de: https://jrvargas.files.wordpress.com/2010/07/tabla-z.pdf
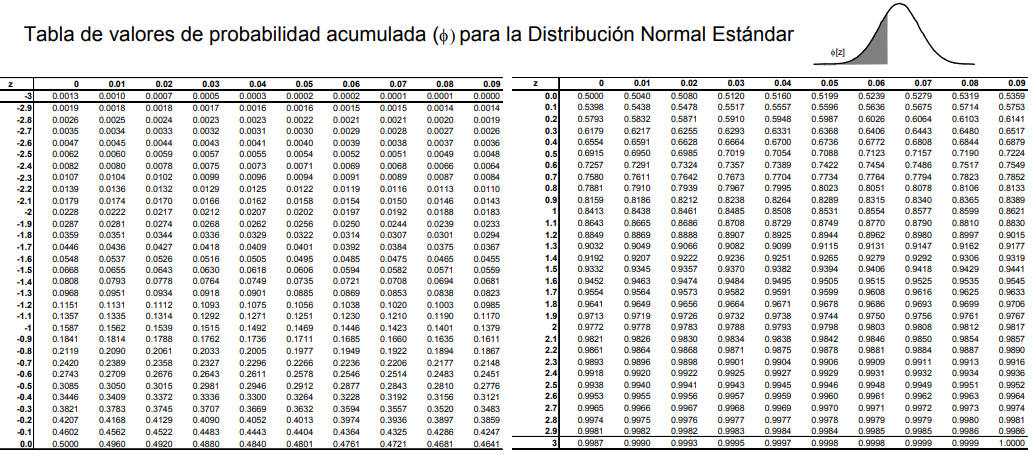
Es claro que la tabla da la distribución normal estándar da la probabilidad acumulada de − ∞ al valor de z indicado. Así para z = 0, la probabilidad dada en la tabla es para P(Z < 0) = 0.5, y para z = − 1.96 la probabilidad es P(Z < − 1.96) = 0.025
Para hallar una probabilidad determinada con las tablas, será necesario hacer el cálculo específico del área involucrada.
Ejemplo. Encontrar la probabilidad a la derecha de z = 1.5
Solución. Esta se interpreta como P(Z > 1.5), cuya gráfica (tomada del programa Geogebra https://www.geogebra.org) :
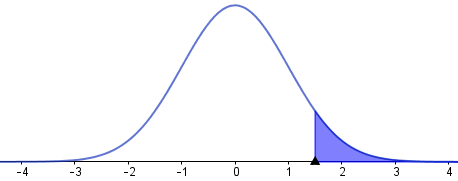
Geogebra da un valor de P(Z > 1.5) = 0.0668, que de las tablas será:
P(Z > 1.5) = 1 − P(Z < 1.5) = 1 − 0.9332 = 0.0668
Además del módulo de cálculos de probabilidad de Geogebra, que permite ingresar los valores de probabilidad requeridos
y grafica en la curva normal el área correspondiente, existen muchos otros paquetes y software. En www.seactuario se ha desarrollado
una calculadora de la Distribución Normal con 4 secciones según el cálculo de probabilidad requerido.
Para el ejemplo, se utiliza la sección I de Distribución Normal Estándar, como se observa en la figura:
 |
Ejemplo 2. Hallar el área de probabilidad entre z = − 1.96 y z = 1.5
Solución. Con geogebra, se tiene la figura siguiente y el resultado es P( − 1.96 < Z < 1.5) = 0.9082
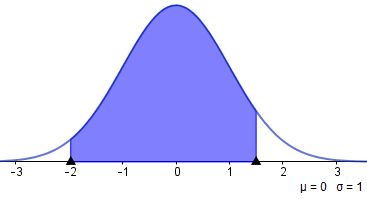
El cálculo con tablas y con la calculadora de sectuario.com, implica:
P( − 1.96 < Z < 1.5) = P(Z < 1.5) − P(Z − 1.96= 0.9332 − 0.025 = 0.9082
Si nos dan la probabilidad de una variable aleatoria normal, nos interesa determinar el valor de z correspondiente. De los ejemplos anteriores ya sabemos que un área de probabilidad de 0.025 a la izquierda corresponde a Z = − 1.96, luego también un área de de probabilidad de 0.025 a la derecha corresponde a Z = 1.96 o también a una probabilidad acumulada de 0.975, como se observa en las figuras generadas con geogebra:
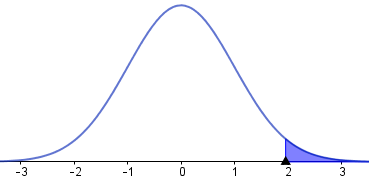 |
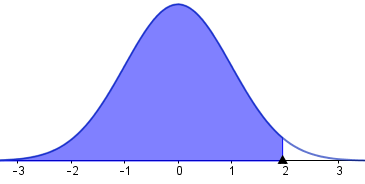 |
| A la derecha de 1.96 se deja un área de 0.025 | A la izquierda de 1.96 se tiene un área de 0.975. |
Ejemplo. Hallar el valor de k tal que P(Z < k ) = 0.8944
Solución. En geogebra se resuelve ensayando valores de z hasta obtener la probabilidad deseada. En tablas, se busca en el área de probabilidad el valor 0.8944 y luego se toman las coordenadas correspondientes a z, como se muestran marcadas en amarillo en la tabla, que corresponde a un valor de z = 1.25
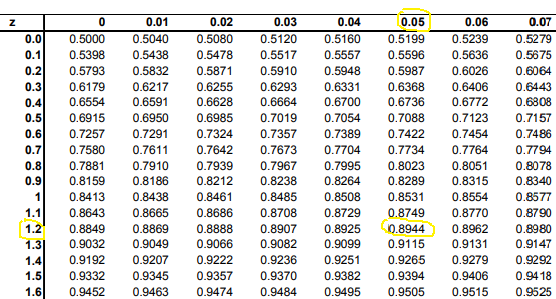
Con la calculadora de la Distribución Normal de www.seactuario.com, se utiliza la sección II, como se observa en la figura:
 |
Ahora evalúese con el Quiz Interactivo - simulación de la Distribución Normal
| Menú Probabilidad y Estadística | D. Discretas: La Poisson | Tema Siguiente | D. Continua Uniforme |