Precálculo
Ingresar E-Learning
Registro
Curso de estadística Aplicada
Análisis de Información con R

INTRODUCCION AL ALGEBRA
Adicionalmente debes distinguir entre las distintas expresiones algebraicas. Existen:- Monomios: los cuales constan de un solo término. a; -b; 1/2cd; -3x2y; abcdef
- Binomios: constan de dos monomios.
Binomios: constan de dos monomios.
Ej: a − b;
1/2cd − 3X2Y;
abcdef + a
Trinomios: constan de tres monomios.
Ej: a − b + 1/2cd;
− 3X2Y + abcdef + a
Polinomios: constan de 4 o más monomios
− 3X2Y + abcdef + a − b + (1/2)cd
SUMA Y RESTA
Sumar y restar algebraicamente es un juego que consiste en que tu identifiques los términos que son semejantes entre sí y de ahí en adelante sumar los coeficientes
EJ. 3b − 10ab + 15a + 8b − 4a − 20ab +12
Entonces sumemos ...
Los que tienen a solamente:
(15 − 4)a = 11a
Los que tienen b solamente:
(3 + 8)b=11b
Los que tienen ab:
(−10 − 20 )ab= −30ab
Los coeficientes solos:
12 no tiene con quien.
Entonces el resultado de sumar el polinomio será:
11 a −30 ab+ 11 b +12
Es conveniente que ordenes la respuesta alfabéticamente y por grado del polinomio de mayor a menor.
MULTIPLICACIÓN
Para multiplicar debes conocer: multiplicación de fraccionarios, leyes de signos, potenciación
(an * am =an+m ) y por supuesto... las tablas de multiplicar
La multiplicación se hace término a término, así podemos tener:
Monomio * Monomio
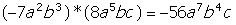 |
Monomio * binomio
(−10abc)(−5ab2 +7c5)= 50a2b3c − 70abc6
Binomio * binomio
(10abc − 7a2b3)( −5ab2 + 7c5)
= (10abc)(−5ab2) + (10abc)(7c5) + (−7a2b3)(−5ab2) + 7a2b3)(7c5)
=−50a2b3c + 70abc6 + 35a3b5 −49a2b3c5
así mismo se pueden tener multiplicaciones de polinomio por polinomio y el principio sigue siendo el mismo, término a término y se suman algebraicamente los exponentes de bases iguales.
ECUACIONES
En una ecuación se afirma que dos expresiones algebraicas son iguales, es decir el lado izquierdo es igual al lado derecho de la misma. En una ecuación el objetivo es encontrar los valores de la incógnita, la cual generalmente (no siempre) se denota por la letra X, que hacen que la ecuación sea verdadera. A estos valores se les conoce como soluciones o raíces de la ecuación.
¿QUÉ TIPO DE ECUACIONES HAY?
En realidad hay muchos tipos de ecuaciones y de métodos de solución, pero aquí nos encargaremos sólo de las polinómicas. De este tipo hay:
Lineales: se reconocen porque el máximo grado (exponente) de la incógnita es 1
Existen ecuaciones lineales con una sola incógnita como:
3X + 8 = 9X − 5
En esta ecuación la incógnita es X, es lineal porque el grado máximo en la expresión para la incógnita es 1; también se pueden tener ecuaciones lineales con más de una incógnita. Ej:
| 2X + 3Y = 5 −7X + Y = 4 |
En el anterior ejemplo las incógnitas son X y Y, pero siguen siendo lineales porque el máximo grado de las incógnitas es 1. En este caso se dice que el sistema es 2x2 (2 ecuaciones con 2 incógnitas). Por lo tanto se pueden tener sistemas de ecuaciones de 3x3, 4x4, nxn Y siempre se estará indicando cuantas ecuaciones y cuantas incógnitas hay.
Los métodos de solución varían dependiendo de la cantidad de ecuaciones que tengas. Así, si es 1x1 (1 ecuación con 1 incógnita), es muy sencillo porque sólo es despejar a X. Pero si es, imagínate por ejemplo 30x30 (30 ecuaciones y 30 incógnitas), pues lo mejor es que consigas un computador que te ayude o que te armes de mucha paciencia para resolver el sistema puede ser por Reducción de Gauss−Jordan.
Cuadráticas: se reconocen porque el grado máximo de la incógnita es 2 y tienen la forma general aX2 + bx + c =0. Mira algunos ejemplos de ecuaciones cuadráticas:
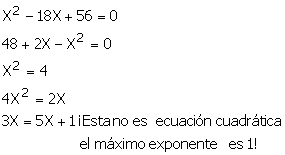 |
La moraleja es: de aX2 + bX + c =0 puede faltar el término bX o c, pero no puede faltar aX2 porque entonces deja de ser cuadrática.
Ahora bien cómo se resuelven.
Pasos:
Se igualan a 0
Se resuelven por casos de factorización:
| Diferencia de cuadrados perfectos | 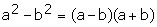 |
| Trinomio Cuadrado perfecto: | 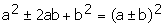 |
| Trinomios de la forma: | 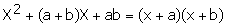 |
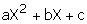 |
En la siguiente sección se profundiza sobre los Casos de Factorización.y solución de ecuaciones.
¿Qué sigue ? Escoja el tema que quiera aprender/repasar:
| Operaciones con Signos de Agrupación |
| Casos de Factorización. |
| Quiz Operaciones con Enteros II |
