APROXIMACIÓN DE LA NORMAL A LA BINOMIAL

Aproximación de la Distribución Normal a la Binomial.

Si X es una variable aleatoria binomial con media μ = np y varianza σ² = np(1 − p), entonces la forma limitante de la distribución:

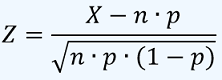
según que n → ∞, es la Distribución Normal Estándar n(z; 0, 1).

Ya que la distribución binomial está concebida para variables aleatorias discretas, y la Distribución Normal para variables continuas, se debe recordar que en esta última la probabilidad de que la variable aleatoria tome un valor exacto es de cero. Luego en esta aproximación para un valor exacto de X en la binomial, se debe calcular en la Normal incrementando el valor de x en 0.5, como se ilustra en el siguiente ejemplo:

Ejemplo. Sea una variable aleatoria discreta X con distribución binomial dada por b(x,20,0.4), luego:

μ = (20)(0.4) = 8, σ² = (20)(0.4)(0.6) = 4.8. La probabilidad de que X tome un valor exacto es igual al área de la barra cuya base se centra en x. Por ejemplo, la probabilidad P(X = 5), que con la calculadora de la binomial es:

P(X = 5) = b(5; 20, 0.4) = 0.0746

y con la aproximación Normal, esta probabilidad es cercana al área entre x₁ = 4.5 y x₂ = 5.5, que al tipificar a valores de Z, son:

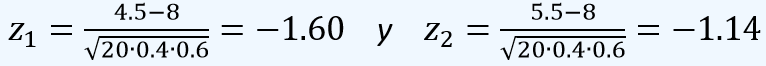
y de esta forma, la probabilidad es:

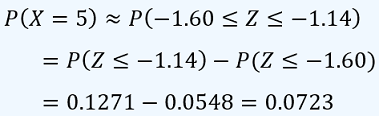
que se aproxima mucho al valor exacto de 0.0746, el error relativo es de (Erelat)_% = (100)(0.0746 − 0.0723)/0.0746 = 3.08 %

El mejor uso de la aproximación de la Normal a la binomial es en el cálculo de sumatorias binomiales para valores grandes de n. Así para calcular en el ejemplo anterior P(8 ≤ X ≤ 10) con la aproximación Normal, tome x₁ = 7.5 y x₂ = 10.5, y luego aplique la tipificación a valores de Z.

Para evaluar la probabilidad P(X ≤ x), se aplica la siguiente fórmula:

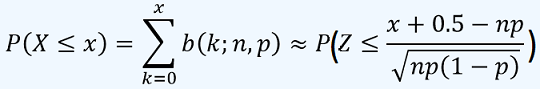
Aplique estos conceptos con el Cuestionario por simulación de la Aproximación de la Normal a la Binomial.