Si ℱ es una familia de eventos de S tal que:
i) ∅ ∈ ℱ
ii) Si A ∈ ℱ entonces Ac ∈ ℱ
iii) Si A1, A2, ..., An ∈ ℱ, entonces
![]()

| Menú Probabilidad y Estadística | Tema Anterior | Tema Siguiente |
Al analizar el Experimento aleatorio: Lanzamiento de un dado corriente tres veces consecutivas, se tiene que los posibles resultados son triplas de la forma (a, b, c), con cada a, b, c ∈ {1, 2, 3, 4, 5, 6}. Esto es:
S = {(a, b, c): a, b, c ∈ {1, 2, 3, 4, 5, 6}}
Se podría construir un diagrama de árbol para especificar los posibles arreglos que describe S. Luego se verán algunas técnicas para hallar estos arreglos.
Una pregunta en este ejemplo es ¿cuál es el "chance" o "posibilidad" de ocurrencia que tiene un "evento", tal como: "La suma de resultados obtenidos es mayor o igual que 14? Sea A el evento de interés, esto es:
A: = {(a,b,c) ∈ S: a + b + c ≥ 14}
A: = {(5,5,4),(4,5,5),(5,4,5),(5,5,5),(6,5,5),(5,6,5),(5,5,6),(6,6,5),(6,5,6),(5,6,6),(6,6,6}
¿Pero qué es un Evento (o Suceso)? Se puede pensar que un Evento es solamente un Subconjunto de un espacio muestral. Lo contrario no es necesariamente cierto, es decir, No todos los subconjuntos de un espacio muestral son Eventos.
Evento o Suceso. Un evento o suceso A (respecto a un espacio muestral S), es un subconjunto de elementos de S. En particular ∅ se denomina el evento imposible y S el evento seguro. Los eventos con un solo elemento se denominan eventos elementales.
Si A y B son eventos, consideraremos los eventos Ac (también se simboliza con A′, ∼A, o Ā ), para los eventos complemento (o negación), A ∪ B, A ∩ B, para el evento unión y evento intersección respectivamente.
La clase de subconjuntos de un espacio muestral S para los que estará definido el "chance" que tienen de ocurrir, debe tener una estructura llamada Sigma Algebra (σ-Algebra), y se representa con ℱ.
| Definición de σ-Algebra ℱ Si ℱ es una familia de eventos de S tal que: i) ∅ ∈ ℱ ii) Si A ∈ ℱ entonces Ac ∈ ℱ iii) Si A1, A2, ..., An ∈ ℱ, entonces
|
Ejemplo 1. Sea S ≠ 0. Entonces ℱ0 = {∅, S} es una σ-Algebra sobre S. Esta es la σ-Algebra trivial.
Ejemplo 2. Sea S = {1,2,3]. Entonces ℱ = {∅, {1}, {2,3}, S} es una σ-Algebra sobre S, en tanto que Β = {∅, {1}, {2}, {3}, S} no lo es. Observe claramente en la primera colección de subconjuntos de S, es decir en ℱ, que el evento ∅ tiene como complemento a S y viceversa; el evento {1} tiene como complemento a {2,3} y viceversa (se cumple la condición ii) de la definición. También la condición iii) se cumple ya que la unión de estos eventos dan toda ℱ. Para la colección Β No se cumple la condición ii).
Ejemplo 3. Consideremos el experimento que consiste en contestar al azar 3 preguntas con "Verdadero" = V o con "Falso" = F. Asociamos a los resultados del experimento el conjunto de todos los posibles resultados, dado por:
S = {(VVV), (VVF), (VFV), (FVV), (VFF), (FVF), (FFV), (FFF)}Observamos que A ∪ B ≠ S, luego para construir la σ-Algebra se requiere al menos un tercer evento, que contenga los demás elementos de S, por ejemplo:
C = (A ∪ B)c = {(FVV),(FFF)}
Luego, ℱ = {∅, A, Ac, B, Bc, C, Cc, S} es una σ-Algebra sobre S.
Ejemplo. Consideremos el experimento aleatorio que consiste en lanzar un dado de quinielas y anotar el símbolo que aparece en la cara superior. Hallar el espacio muestral y el espacio de sucesos o σ-Algebra
|
Espacio muestral: S = {1,X,2} Espacio de sucesos: ℱ = {Ø,{1},{X},{2},{1,X},{1,2},{2,X},{1,X,2}} |
 |
Existen algunas definiciones de Probabilidad que el Actuario debe manejar. Entre estas se encuentran la Definició,n clásica de Probabiidad y la definición axiomática. Para llegar a estas veremos algunos otros conceptos
| Definición. Espacio Medible. Sean un espacio muestral S ≠ ∅ y ℱ una σ-Algebra sobre S. La pareja (S, ℱ) se llama espacio medible. |
Es claro según la definición, que S y ∅ pertenecen a cualquier σ-Algebra ℱ sobre S. S se llama evento seguro, es decir que tiene el 100% de "chances" de ocurrir y ∅ se llama evento imposible. Un evento de la forma {s} con s ∈ S se llama evento elemental.
Decir que un evento A ocurre, significa que el resultado obtenido (al realizar el experimento aleatorio con espacio muestral S) es una elemento de este evento A. De esta forma, si A y B son eventos, entonces en términos del "chance" de ocurrir:
i) A ∪ B es un evento que ocurre, si y sólo si, A o B o ambos eventos ocurren.
ii) A ∩ B es un evento que ocurre, si y sólo si, si A y B ocurren.
iii) Ac es un evento que ocurre, si y sólo si, si A no ocurre.
iv) A − B es un evento que ocurre, si y sólo si, A ocurre pero no B.
El objetivo ahora es asginar a cada evento A, un número real no negativo que indique el "chance" que tiene A de ocurrir. Supóngase que se realiza un experimento n veces bajo las mismas condiciones.
| Definición. Frecuencia relativa. Para cada evento A, el número |
Ejemplo. Se lanza una moneda 100 veces y se obtiene como resultado "sello" en 60 de estos lanzamientos. Entonces las frecuencias relativas de los eventos A: = "El resultado es sello", y B: = "El resultado es cara" en este experimeto aleatorio, son respectivamente 3/5 y 2/5 respectivamente.
Se lanza un dado común 500 veces y se obtienen 90 veces el resultado 5. Para este experimento aleatorio la frecuencia relativa del evento A. "El resultado es 5" es igual a 9/50. Y el resultado del evento Ac: ="El resultado no es 5" es Ac: = 41/50.
En el experimento aleatorio de lanzar un dado común un número n de veces, y sea el evento:
A: = "el resultado obtenido es 5".
Se tomaron los datos que se observan en la siguiente tabla, con f para la frecuencia absoluta hasta el valor n especificado y fr para la frecuencia relativa.
| n | f | fr |
|---|---|---|
| 100 | 13 | 0.13 |
| 200 | 29 | 0.145 |
| 300 | 51 | 0.17 |
| 400 | 66 | 0.165 |
| 500 | 83 | 0.166 |
La establización de la frecuencia relativa a un determinado valor (en el límite a medida que n es suficientemente grande), es lo que se conoce como "regularidad estadística" y es lo que nos permite realizar predicciones sobre situaciones aleatorias y eliminar parcialmente la incertidumbre presente en los fenómenos impredecibles.
El valor P(A) alrededor del cual se estabiliza la frecuencia relativa de un evento, indica el "chance" o "probabilidad" que tiene este de ocurrir. Algunas propiedades fundamentales de este número P(A) son:
- En primer lugar como n(A) ≥ 0 entonces P(A) debe ser también mayor o igual que cero
Como n(S) = n, entonces fr(S) = 1 y en concecuencia P(S) = 1
Si A y B son dos eventos mutuamente excluyentes, esto es, P(A ∩ B) = 0, entonces se satisface que n(A ∪ B) = n(A) + n(B) y por lo tanto fr(A ∪ B) = fr(A) + fr(B). Esto implica que P(A ∪ B) = P(A) + P(B)
Antes de utilizar estas observaciones para dar la definición de espacio de probabilidad, veamos otras formas, que las llamaremos relgas en vez de definiciones de probabilidad, pero que son muy útiles:
| Regla. Si un experimento puede dar como resultado cualquiera de N diferentes resultados que tienen las mismas probabilidades de ocurrir, y si exactamente n de estos resultados corresponden al evento A, entonces la probabilidad de evento A es
|
Esto también se puede expresar como
| "La probabilidad de un evento A es el cociente entre
el número de casos favorables al evento y el número de casos posibles". Si indicamos la probabilidad del evento A por P(A), podemos expresar esta definición como:
|
Ejercicios Resueltos
1. Se considera un experimento aleatorio que consiste en lanzar un dado se pide
la probabilidad de obtener:
a) Número impar
b) Número primo
c) Múltiplo de 3.
d) Múltiplo de 5.
Primeramente formamos el espacio muestral del experimento:
E ={ 1,2,3,4,5,6}
Luego el número de casos posibles es 6.A continuación formamos los sucesos cuya probabilidad nos piden:
a) A= " obtener impar" = {1,3,5}→ p(A) = 3/6
b) B= " obtener número primo" = {2,3,5} → p(B) =
3/6
c) C= " obtener múltiplo de 3" = {3, 6}→ p(B) =
2/6
d) D ="obtener múltiplo de 5 " = {5} → p(D)=
1/6
2. se realiza un experimento aleatorio que consiste en la extracción de una
carta de una baraja española .Se pide hallar las siguientes probabilidades:
a) "Obtener un oro"
b) "Obtener un as"
El espacio muestral del experimento está formado por los 40 resultados
posibles correspondientes a cada una de las cartas de la baraja. A continuación
formamos los sucesos de los cuales nos piden estimar la probabilidad.
a) O = "Obtener un oro" = {1,2,3,4,5,6,7,S, C, R} →
p (O) = 10/40 = 1/4
b) A = "Obtener un as" = { 1E, 1C, 1B,10}
→ p (A) = 4/40 = 1/10
En este caso los súbíndices son E =Espada, C = Copas, B = Bastos, O = Oro
3. Consideremos el experimento aleatorio que consiste en lanzar dos dados y
anotar la suma de los puntos de las caras superiores. Hallar la probabilidad de
los siguientes eventos:
a) Obtener suma de igual a 8 .
b) Obtener suma menor o igual a 4
Primeramente construimos el espacio muestral del experimento:
E= {(1,1),(1,2), (1,3),..,(2,2), (2,3),...,(6,1),...,(6,6)}
Por tanto, el número de casos posibles es 36.
A continuación formamos los eventos cuya probabilidad nos piden :
a) S8 = {(2,6), (3,5), (4,4), (5,3), (6,2)}→ p (S8)
= 5/36
b) S≤4= {(1,1), (1,2), (1,3), (2,1),(2,2),(3,1)}
→ p ( S≤4)
=6/36 = 1/6
Un modelo probabilístico es una descripción matemática de una situación incierta. Sus principales ingredientes se listan a continuación y se visualizan en la figura
| Elementos de un modelo de probabilidad - El espacio muestral S, que es el conjunto de todos los posibles resultados de un experimento aleatorio. - La Ley de Probabilidad, que asigna a un evento A de posibles resultados, un número no negativo P(A) que se llama la probabilidad de A que cuantifica el "chance" de que ocurra A. |
|
| Espacio de Probabilidad. Sea (S, ℱ) un espacio medible. Se llama probabilidad a una ley (función o aplicación) P definida sobre ℱ, que asocia a cada evento A un número real que
llamamos probabilidad de A y representamos por P(A), que cumple las siguientes condiciones : i) la probabilidad de un evento cualquiera es positiva o nula: P(A) ≥ 0, para todo A ∈ ℱ ii) la probabilidad del evento cierto es igual a la unidad :P(S) = 1 iii) la probabilidad de la unión de dos eventos incompatibles (o mutuamente exluyentes) es igual a la suma de las probabilidades de cada uno de ellos.Si A y B son incompatibles, P(A ∪ B) = P(A) + P(B). O en forma general, para cualquier número de eventos:iii) Si A1, A2, ... ∈ ℱ,y son eventos mutuamente excluyentes, esto es: Ai ∩ Aj = 0 para todo i ≠ j. entonces
|
|
 |
|
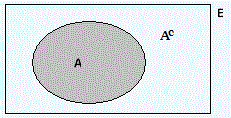
En efecto, como A ∪ Ac = S y además A y Ac son incompatibles, resulta:
| 1 = P(S) = P(A ∪ Ac ) = P(A) + P(Ac ), de donde, P(Ac ) = 1 − P(A) |
En muchas ocasiones , el calculo de la probabilidad del suceso contrario
Ac es más fácil que el de A. En estos casos es conveniente calcular primero la
probabilidad P(Ac ) y a continuación aplicar la fórmula P(A) = 1 − P(Ac ).
2. probabilidad del suceso imposible
la probabilidad del suceso imposible es cero.
|
P(∅) = 0 |
En efecto, como el suceso imposible es el contrario del suceso cierto y P(S ) = 1, por el axioma segundo se tiene:
| P(∅ ) = 1 − P(S) = 1 − 1 = 0 | ||||||
3. Relación entre las probabilidades de dos eventos cuando uno está
contenido en otro
| Si un evento A está contenido en otro evento B, entonces P(A) es menor o igual a P(B), es decir : |
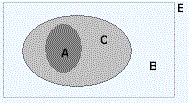 |
| P(A) ≤ P(B) |
Ejercicios de práctica: Ejercicio 3 Ejercicio 4 Quiz sobre probabilidades
| Menú Probabilidad y Estadística | Tema Anterior | Tema Siguiente |