se actuario

PROBABILIDAD: REGLAS DE PROBABILIDAD

Menú Probabilidad y Estadística Tema Anterior Tema Siguiente

26. Reglas de Probabilidad para Eventos Compuestos

26.1 Reglas Aditivas

Frecuentemente resulta más fácil calcular la probabilidad de un evento en particular a partir de las probabilidades conocidas de otros eventos. Esto puede ser cierto si el evento de interés se puede representar como la unión de otros dos eventos o como el complemento de algún evento. Se presentan a continuación varias reglas importantes que a menudo simplifican el cálculo de las probabilidades. La primera es la Regla Aditiva que se aplica a la Unión de Eventos. Teorema. Regla de la Disyunción. Si A y B son dos eventos, entonces
P(A∪B = P(A) + P(B) − P(A∩B)

disyuncion

Prueba: Observe el diagrama de Venn de la figura anterior. P(A∪B) es la suma de las probabilidad de los puntos muestrales en (A∪B). Así, P(A) + P(B) es la suma de todas las probabilidad en A más la suma de las probabilidad en B. Por lo tanto, se están sumando dos veces las probabilidad en (A∩B). Como estas probabilidades se suman a P(A∩B), se debe restar esta probabilidad una vez para obtener la suma de las probabilidades en (A∪B).
Veamos ahora varios ejemplos de aplicación.
- Ejemplo de Unión de sucesos: Lanzamiento de un dado.

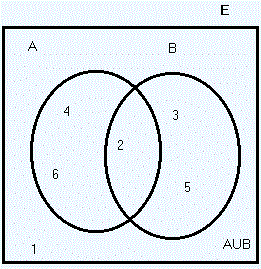A ∪ B={2,3,4,5,6}

Consideremos , en el experimento aleatorio del lanzamiento del dado, cuyo espacio muestral es
S = {1,2,3,4,5,6}, y ahora los siguientes eventos:

A ="salir número par" = {2,4,6}. Luego P(A)= 3/6 = 1/2

B = "salir número primo" ={2,3,5}. Luego P(B)= 3/6 = 1/2

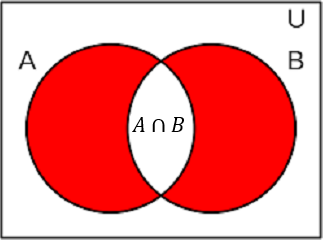
(A∩B) = Salir número par Y primo = {2}. Luego P(A∩B)=1/6

Formemos el suceso C, "salir número par  o  numero primo". Este suceso es

C = (A∪B) = {2,3,4,5,6}. Luego P(A∪B)= 5/6

y se varifica mediante la Regla de la Suma o Disyunción que:

P(A∪B) = P(A) + P(B) + P(A∪B)= 1/2 + 1/2 - 1/6 = 5/6.

Corolario. Si A y B son mutuamente excluyentes, entonces

P(A∪B) = P(A) + P(B)

Si A y B son mutuamente excluyentes, entonces (A∩B) = 0 y por consiguiente P(A∩B) = P(∅) = 0.

En general para cualquier cantidad de eventos mutuamente excluyentes:

Si B1, B2, ..., Bn son mutuamente excluyentes, entonces

P(B1 ∪ B2 ∪ ... ∪ Bn) = P(B1) + P(B2) + ... + P(Bn)

Partición

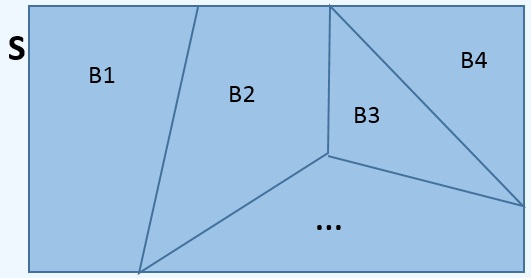
Un conjunto de eventos {B1 ∪ B2 ∪ ... ∪ Bn} de un espacio muestral S se considere una partición del espacio muestral S, si B1, B2, ..., Bn son mutuamente excluyentes, esto es, Bi∩Bj = 0, y colectivamente exhaustivos, esto es, B1 ∪ B2 ∪ ... ∪ Bn = S.

Por lo tanto se tiene que:

Si B1, B2, ..., Bn es una partición de un espacio muestral S, entonces

P(B1 ∪ B2 ∪ ... ∪ Bn) = P(B1) + P(B2) + ... + P(Bn) = P(S) = 1



Ahora resuelva un Ejercicio Interactivo de una Partición

El teorema de Disyunción para tres eventos es de la forma:

Para tres eventos A, B y C,

P(A ∪ B ∪ C) = P(A) + P(B) + P(C) − P(A ∩ B) − P(A ∩ C) − P(B ∩ C) + P(A ∩ B ∩ C)

La demostracion es:

disyuncion 3 eventos

Ejercicios de práctica: Ejercicio 3          Ejercicio 4         Quiz sobre probabilidades

Menú Probabilidad y Estadística Tema Anterior Tema Siguiente