
| Menú Probabilidad y Estadística | Tema Anterior | Tema Siguiente |
| (n)n = |
|
La cantidad (n)n es n factorial y se expresa en matemáticas como
n!. Por ejemplo 5! = 5 X 4 X 3 X 2 X 1 = 120. Recuerde que 1! = 0! = 1
De esta forma una permutación es un arreglo de todos o parte de un conjunto de objetos. Arreglos que se puedan
distinguir:
a. Si se quieren arreglar objetos, donde todos los objetos sean diferentes entre
sí, la permutación (el número de arreglos que se pueden obtener) es n ! (n
factorial)
Veamos un ejemplo :
Ejemplo 1:
Cinco amigos que están en una piscina, después de haberse lanzado por el deslizadero gigante, observan que cada vez que llegan a la parte superior para el nuevo lanzamiento hacen cola en distinto orden. ¿De cuántas formas podrán hacer cola para arrojarse de nuevo?
Observe que para la primera posición hay cinco personas, cuatro para la segunda, etc.
De esta forma tenemos que el número de formas distintas de hacer cola es:
V5,5 = 5! = 5·4·3·2·1 = 120
Como observamos, en este caso intervienen a la vez todos los elementos y únicamente varía el orden de colocación.
Ejemplo 2: Queremos permutar (arreglar) las letras abc. Cuáles arreglos se obtienen ?
abc, acb, bac, bca, cab y cba . Son 6 permutaciones diferentes. También
hubiéramos podido decir :
Son 3 letras diferentes a, b y c por lo tanto son 3 ! (3 factorial)
permutaciones
3 ! = 3·2·1 = 6
Vemos que hay efectivamente 3 opciones para la primera posición
(cualquiera de las letras a,b o c), luego quedan sólo dos opciones
para la segunda posición (por ejemplo si se escogió a para la primera
posición, quedarían b o c para la segunda posición), y quedaría
una sola letra para la tercera posición.
| Permutaciones ordinarias de n elementos son los distintos
grupos que se pueden formar de manera que: - En cada grupo (o lista) están los n elementos. - Un grupo se diferencia de otro únicamente en el orden de colocación de los elementos. El número de permutaciones ordinarias de n elementos se representa por Pn y es igual a n! |
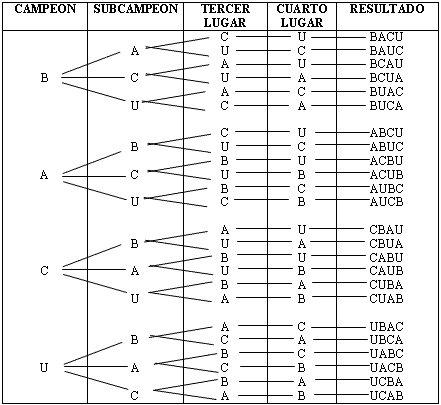
Ejemplo 3:
En un campeonato suramericano de Fútbol llegan a un cuadrangular final los cuatro seleccionados de Brasil, Argentina, Colombia y Uruguay. Formar las diferentes clasificaciones para los cuatro primeros puestos del torneo. ¿Cuántas hay?
Representamos por sus iniciales a cada seleccionado y mediante un diagrama de árbol se obtiene:

De aquí vemos que hay : P4 = 4! = 4·3·2·1 = 24 clasificaciones distintas.
b. Las variaciones sin repetición también se pueden representar con factoriales,
según: Si se quieren arreglar n objetos diferentes, pero se van a tomar
r objetos de
ellos los cuales son distinguibles entre sí, entonces :
| Vn,r = |
|
Ejemplo : De
cuántas formas puede seactuario.com colocar a 3 programadores de sistemas en 3
diferentes ciudades. Si los programadores están disponibles para cualquiera de 5
ciudades.
Entonces se tienen 3 programadores disponibles pero hay 5 posibles ciudades a
donde ellos pueden ir. ¿De cuántas formas podríamos ubicarlos?
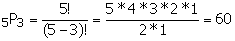 |
Cmo las dos letras siempre van a estar juntas y en el mismo orden, las podemos considerar como si fuera una sola letra. Por esta razón es una permutación realmente de sólo siete elementos:
P7 = 7! = 7·6·5·4·3·2·1 = 5040 palabras diferentes
Ejemplo: ¿De cuántas formas se pueden sentar nueve personas en una mesa circular?
Hay que tener en cuenta que una vez sentadas, si trasladamos a cada persona un asiento a la izquierda obtendremos una posición idéntica a la anterior. Por ello dejamos fija una persona y permutamos todas las demás:
P8 = 8! = 8·7·6·5·4·3·2·1 = 40320 formas distintas
A estas permutaciones se las denomina permutaciones circulares de n elementos y se representan por PCn.
Si se quiere permutar (arreglar) objetos, dentro de los cuales hay varios
repetidos, entonces se pueden contar las posibilidades de arreglos diferentes
usando:
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Pero si se intercambian las dos primeras bombillas amarillas entre sí vemos:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
¡ No se aprecia el cambio ! Por lo tanto, ese cambio no cuenta como arreglo, de modo que al aplicar la fórmula anterior se descuentan todos esos arreglos que son iguales entre sí, de forma tal que las posibilidades de arreglos diferentes que se tienen son:
| |
Ejemplo: Imaginemos que tenemos 5 monedas de 100 centavos, de las cuales dos están en posición de cara y tres en posición de cruz. ¿Cuántas ordenaciones diferentes podremos formar en las que siempre estén dos en posición de cara y tres en posición de cruz?
Las ordenaciones posibles son:
| CCXXX |
| CXCXX |
| CXXCX |
| CXXXC |
| XCCXX |
| XCXCX |
| XCXXC |
| XXCCX |
| XXCXC |
| XXXCC |
Si las monedas son distinguibles tendríamos: P5 = 5! =120 formas distintas
Pero como son del mismo tipo de moneda, sólo se deben considerar una por cada 2!·3! = 12. En consecuencia, de las 120 permutaciones ordinarias iniciales solo tendremos:
| 120 = | 5! = 10 |
| 12 | 2!·3! |
Esta es una permutación con repetición de cinco elementos, donde uno se repite tres veces y otro dos veces.
Definición y número de permutaciones con repetición.
|
||||||||||||
Ejemplo: El mismo caso de las monedas pero ahora con un total de 11 monedas en las que 6 están en posición de cara y 5 en posición de cruz. El número de ordenaciones posibles es de:
| 11! = | 11·10·9·8·7·6! = 462 |
| 6!·5! | 6!·5·4·3·2·1 |
Ejercicio: Un apostador tiene el presentimiento de que en la próxima jornada futbolística (en un torneo nacional con 28 equipos) ganarán 9 equipos en casa, empatarán 3 y ganarán en campo contrario (de visitantes) 2. ¿Cuántas apuestas deberá realizar para asegurarse un pleno de 14?
Sln. / Se trata de las permutaciones de 14 elementos, entre los cuales:
- El elemento 1 aparece 9 veces (ganadores locales)
- El elemento 2 aparece tres veces (empates)
- El elemento 3 aparece 2 veces (ganadores de visitante).
Las permutaciones son:
| 14! = | 14·13·12·11·9! = 20020 apuestas |
| 9!·3!·2! | 9!·6·2 |
Algunas veces estamos interesados en seleccionar sin orden específico r objetos de un total n. A esa selección se le denomina combinación Cn,m:
|
|
Cn,m = |
|
= Vn,m | |
| Pr |
.
Miremos un ejemplo:
Supongamos que se quiere escoger 3 ingenieros químicos dentro de un grupo de 8.
Aclaremos además, que este procedimiento implica escoger al azar a estas 3
personas, sin ningún tipo de preferencia o condicionamiento por o hacia alguno
de ellos. Entonces las formas de seleccionar a los 3 ingenieros de 8 posibles
serán:
|
|
Hay 56 formas de seleccionar a los 3 ingenieros.
Ejemplo:
En una frutería ofrecen entre sus productos distintas mezclas con zumos de frutas. El cliente puede seleccionar entre 6 zumos de frutas diferentes y obtener algún sabor en particular de la mezcla de dos zumos en partes iguales. ¿Entre cuántos sabores distintos puede el cliente hacer su pedido?
Sln/ Vamos a representar cada zumo con las letras A, B, C, D, E y F. Al mezclar dos zumos y teniendo en cuenta que el orden no influye, se podrían obtener los siguientes sabores:
| AB | BC | CD | DE | EF |
| AC | BD | CE | DF | |
| AD | BE | CF | ||
| AE | BF | |||
| AF |
Es decir, 15 sabores diferentes.
| AB | BC | CD | DE | ||||||
| AC | BD | CE | DF | ||||||
| AD | BE | CF | |||||||
| AE | BF | ||||||||
| AF |
Luego C6,2 = 15
¿Cómo podemos obtener este resultado matemáticamente?. Como vimos de la definición: Cn,m = Vn,m / Pn
Donde V6,2 =6! / (6-2)! = 6!/ 4! = 30
y: P2 = 2! = 2
De aquí:
C6,2 = 30 / 2 = 15
¿Qué pasa si se deciden ofrecer sabores combinando 3 zumos de frutas?En este caso tendremos C6,3, aplicando la ecuación directamente tendremos:
|
C6,3 = |
6! = | 6·5·4·3! | = 20 |
| (6-3)!·3! | 3!·6 |
Es decir 20 sabores diferentes.
Ejemplo:
Como respuesta a un anuncio de trabajo se presentan 15 personas para cubrir tres cargos administrativos. ¿Cuántos grupos diferentes de tres personas se pueden formar?
Sln:/ Teniendo en cuenta que para este caso en particular no influye el orden, se trata de una combinación C15,3:
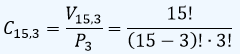 |
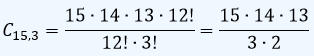 |
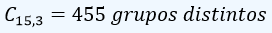 |
b. ¿Cuántos grupos diferentes de tres personas se pueden formar si se retiran tres de los aspirantes?
Rta: 220 grupos distintos
Ejemplo:Cuántos triángulos distintos se pueden formar con ocho puntos en el plano si nunca hay tres de ellos alineados?
Sln./ Para que dos triángulos sean distintos, se tienen que diferenciar al menos en un vértice. Por consiguiente, como no influye el orden en que se tomen los vértices, el número de triángulos distintos que se puede formar es C8,3.
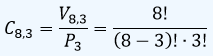 |
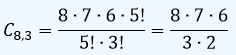 |
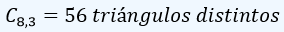 |
Veamos algunos ejemplos adicionales de lo que hemos visto.
1.
a. Encontremos los arreglos diferentes que se pueden hacer con las letras de la
palabra PESO
En este caso de trata de una permutación de cuatro letras diferentes, todas
distinguibles entre sí.
En este caso es como si tuviéramos 4 casillas disponibles para colocar en ellas
las letras
|
= 24 arreglos |
b. Permutaciones con la palabra VACA.
Se tienen nuevamente cuatro letras pero esta vez dos de ellas son iguales y no
se pueden distinguir entre sí, por lo tanto se deben descontar los arreglos que
se vean iguales entre sí:
| |
Si se hiciera el conteo de cada uno de ellos solo serían distinguibles entre sí, 12 .
2. Cuántos números de 3 dígitos se pueden formar con los 6 números {1,3,4,5,6,7,8}.
a. Si no se admiten repeticiones: para este ejemplo la forma de
resolver el ejercicio es igual al planteado anteriormente: se tienen 6 números
para colocar sólo en tres casillas. En una primera casilla puede ir cualquiera
de los 7 números, en la segunda quedan cualquiera de 6 disponibles (no se admite
repetir número) y en la última casilla cualquiera de 5
|
= 210 posibles numeros de 3 dígitos |
Para aclarar un poco más el ejemplo basta entender que al no
admitir repetición de números, entonces el número de 3 dígitos 355 no es válido
según la restricción impuesta debido a que el 5 se repite y esto no se acepta.
b. Con repetición: si este es el caso, entonces en cada una de las casillas puede ir cualquiera de los 7 números disponibles ya que las repeticiones sí son aceptadas.
Entonces:
|
= 343 números posibles, incluyendo también | |||
| los que tienen cifras repetidas |
c. Si se quiere que sean pares sin repeticiones: dentro de los números dados las
posibilidades son que terminen en 4, en 6 o en 8, por lo tanto sólo hay 3
opciones para el último dígito y tras haber fijado este número sólo quedarían 6
números disponibles (no se admiten repeticiones) para la primera casilla y 5
para la segunda.
Entonces:
|
= 90 posibles numeros pares |
|
= 147 posibles numeros pares |
3. En un talego hay 6 balotas blancas y 5 verdes.
a. Encontremos el número de formas de sacar 4 balotas del talego si pueden ser
de cualquiera de los dos colores.
En este caso se va a realizar una selección, en ella no interesa el orden y sólo
se trata sacar las balotas sin importar el color. Este es un ejercicio típico de
combinación (selección) donde se busca sacar 4 balotas de 11.
Entonces:
| |
| |
hay 150 maneras de sacar 2 balotas blancas y 2 verdes
| Menú Probabilidad y Estadística | Tema Anterior | Cuestionario Técnicas de Conteo |