DISTRIBUCION DE DENSIDAD DE PROBABILIDAD (CASO: VARIABLE ALEATORIA CONTINUA)

Una variable aleatoria continua tiene una probabilidad 0 de tomar exactamente cualquiera de sus valores, por lo cual la distribución de probabilidad no se puede presentar en tablas. Supongamos que se le pide que elija un número al azar del intervalo [0, 1] con todos los números en el intervalo con las mismas probabilidades. El número X que usted elige es una variable aleatoria, ya que es una cuantificación numérica cuyo valor depende de la casualidad. Sin embargo, X no es discreto. El intervalo [0, l] es continuo, y puede elegir cualquier número del mismo. X es por lo tanto continuo.

Las probabilidades para las variables aleatorias continuas se calcularán de otra forma. El método de probabilidad continua se ilustra muy bien mirando en la variable aleatoria X del espacio muestral en el intervalo [0, 1]. Por ejemplo, supongamos que desea calcular la probabilidad P(0.50 < X < 0.75). Intuitivamente, se puede suponer que esta probabilidad es 0.25, ya que el 25 % de los números en el intervalo [0, l] están entre 0.50 y 0.75.

El método que se utiliza para evaluar las probabilidades de una variable aleatoria continua, implica el problema de cálculo integral de encontrar áreas bajo las curvas. La función de distribución f(x) nos da la curva correspondiente, es decir, como una fórmula, y el área se evalúa en un determinado intervalo. Por lo cual es de interés No el cálculo de la probabilidad de tomar un valor específico, sino la probabilidad de que la variable aleatoria tome un intervalo como P(a < X ≤ b), P(X > c) o P(X < d).
De esta forma, ya que los extremos del intervalo de interés para evaluar la probabilidad cuando X es continua no importa (lo cual no es cierto si la variable es discreta), se tiene que:

P(a < X ≤ b) = P(a < X < b) + P(b) = P(a < X < b)

Definición. La función f(x) es una función de densidad de probabilidad (fdp) para la variable aleatoria continua X, definida en el conjunto de números reales, si i. f(x) ≥ 0 ii. iii.

Observaciones. Es claro que si x tiende a infinito, entonces la integral es 1, además f(x) es una función no negativa y juega un papel muy similar al de la función de probabilidad en el caso discreto. La diferencia importante que se debe notar es que en el caso discreto f(x) = P(X = x) mientras en el caso continuo P(X = x) = 0 y f(x) no indica probabilidad, y más aún, f(x) puede ser mayor que 1.

Ejemplo: Para el caso mencionado, sea la función de densidad de probabilidad de la variable aleatoria continua X

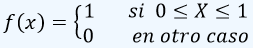
Al calcular la probabilidad P(0.50 < X < 0.75) encontrando el área limitada por la curva de f(x) y el eje x entre x = 0.5 y x = 0.75, como se ilustra en la siguiente figura:

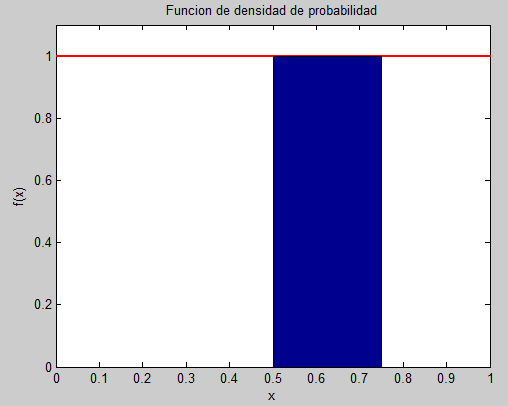
el área deseada es 0.25, lo cual nos da la probabilidad P(0.50 < X < 0.75) como el 25% de los números de interés en el intervalo [0, 1] como ya se había mencionado. También se podría calcular como la integral. Por ejemplo si ahora interesa hallar la probabilidad P(0.10 < X < 0.70), se tiene:

Ejemplo. Compruebe si f(x) = e^−x, es una función de densidad de probabilidad, si se establece como

Si lo es, halle P(1 ≤ X ≤ 3)

Solución. La gráfica de la función es,

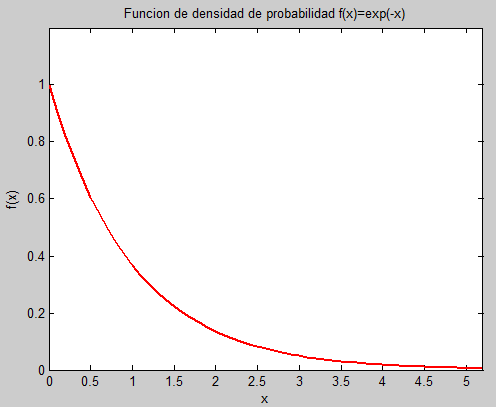
Para comprobar si se trata de una función de densidad, se realiza la integral en todo el dominio de los números reales:

Luego, para encontrar la probabilidad P(1 ≤ X ≤ 3), lo cual gráficamente se representa como

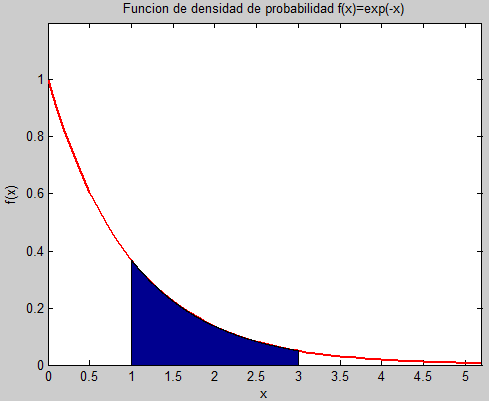
y el cálculo de esta probabilidad es

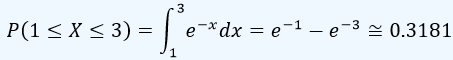
Es momento de practicar con nuestro Ejercicio interactivo de Funcion de Densidad de Variables Aleatorias Continuas