Definición. La función de distribución acumulativa F(x), de una variable aleatoria continua X con función de densidad f(x), es
|

| Menú Probabilidad y Estadística | Tema Anterior | Tema Siguiente |
La definición de F(x) es la misma para variables aleatorias discretas o continuas, pero los cálculos para el caso continuo utilizan la integración en vez de las sumatorias.
Definición. La función de distribución acumulativa F(x), de una variable aleatoria continua X con función de densidad f(x), es
|
La función de distribución acumulada F(x) es una función continua para todo x en los reales.
Geométricamente, F(x) es el área bajo la gráfica de su correspondiente función de densidad f(x) a la izquierda de x. De esta forma, para la función de densidad exponencial

La función de distribución acumulada F(x), gráficamente, es:

Así, si en la gráfica anterior x = 2.75, entonces F(X = 2.75) = F(2.75) = P(X ≤ 2.75) , que resulta
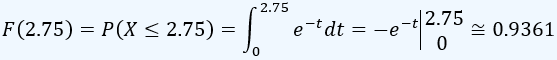
La función F(x) es creciente, continua y ya que da la probabilidad hasta cierto valor x, es positiva. Para la función de densidad f(x)= e−x, la función de distribución F(x) es:

Al graficar la función de Distribución acumulativa F(x)= 1 − e−x, que corresponde a la función de densidad f(x)= e−x, resulta:
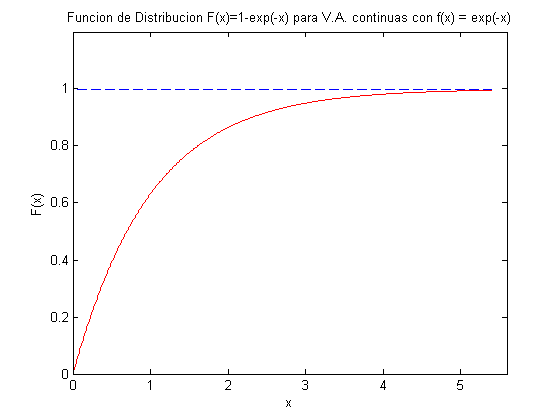
Y así mismo al calcular F(2.75) = 1 − e−2.75 = 0.9361, como en el caso anterior, pero ahora se podría leer directamente de la última figura con x = 2.75 en el eje x y el valor correspondiente de F(2.75) = 0.9361 sobre el eje vertical. O como se muestra en la siguiente figura para F(3) que corresponde a un valor de 0.95
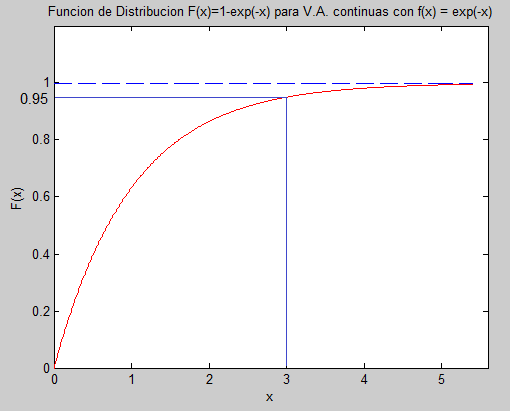
Propiedades de la Función de Distribución Acumulada a) 0 ≤ F(t) ≤ 1 b) F'(t) = f(t). c) F(t)es una función Creciente, así si a < b entonces F(a) ≤ F(b) d) F'(t) = f(t). e) F(t) → 0 en cuanto t → −∞ y F(t) → 1 en cuanto t → ∞ b) P(a < X ≤ b) = F(b) − F(a). |
| Menú Probabilidad y Estadística | Tema Anterior | Tema Siguiente |