Definición.Para una variable aleatoria discreta, la función de distribución acumulada F(x), con distribución de probabilidad f(x) es 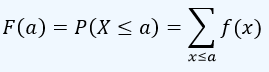 |

| Menú Probabilidad y Estadística | Tema Anterior | Tema Siguiente |
Existen muchos problemas en los que se desea calcular la probabilidad de que el valor observado de una variable aleatoria X esté por debajo o sea igual a algún valor x. Al escribir F(x) = P(X ≤ x) para cualquier número real x, se define F(x)como la función de distribución acumulativa de la variable aleatoria X
Todas las variables aleatorias (discretas y continuas) tienen una función de distribución o función de distribución acumulativa , abreviado fda o cdf en Inglés (cumulative distribution function).
Definición.Para una variable aleatoria discreta, la función de distribución acumulada F(x), con distribución de probabilidad f(x) es 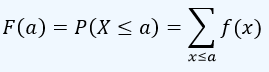 |
Como se observa, F(x) es una función que da la proporción de valores de X menores o iguales que x, para cada valor x. Se encuentra sumando todas las probabilidades hasta el valor x.
Si X es una variable aleatoria (v.a.) con f.d.a F(x), entonces:
⛧ P(X ≤ b) = F(b)
⛧ P(a < X ≤ b) = F(b) − F(a)
⛧ P(X < b) = limx ↦ b- F(x) = F(b-)
⛧ P(a < X < b) = limx ↦ b- F(x) − F(a) = F(b-) − F(a)
Propiedades de la f.d.p. F(x). La f.d.p. F(x) de una v.a. X, satisface las siguientes propiedades:
(i) F(x) es una función creciente
(ii) limx ↦ -∞ F(x) = 0
(iii) limx ↦ ∞ F(x) = 1
(iv) F(x) es continua a la derecha.
Observación: Al definir F(x) y de acuerdo a las propiedades anteriores, esta es una función definida a trozos, escalonada creciente y el dominio se debe definir en todos los reales.
Ejemplo. Del experimento que consiste en responder al azar tres preguntas con Verdadero o Falso (V / F) y con la variable aleatoria definida como el número de respuestas marcadas con V. X toma los valores 0, 1, 2 o 3, es decir, el rango de la función (variable aleatoria) X es el conjunto {0, 1, 2, 3}. Encontrar a) la función de probabilidad y b) la función de distribución.
Solución. El espacio muestral S = {(FFF),(FFV), (FVF), (VFF), (FVV), (VFV), (VVF), (VVV)}, así a) La función de probabilidad es:
| (x) | 0 | 1 | 2 | 3 |
| f(x) = P(X=x) | 1/8 | 3/8 | 3/8 | 1/8 |
y b)La función de Distribución es:
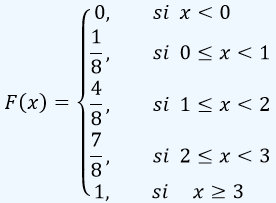
De donde según la definición de la función de Distribución Acumulada,
F(0) = P(X ≤ 0) = f(0) = 1/8
F(1) = P(X ≤ 1) = f(0) + f(1) = 1/8 + 3/8 = 4/8 = 1/2
F(2) = P(X ≤ 2) = f(0) + f(1) + f(2) = 1/8 + 3/8 + 3/8 = 7/8
F(3) = P(X ≤ 3) = f(0) + f(1) + f(2) + f(3) = 1/8 + 3/8 + 3/8 + 1/8 = 1
La gráfica de una Función de Distribución Acumulada de una Variable Discreta, es escalonada y creciente. Para el ejemplo, es:
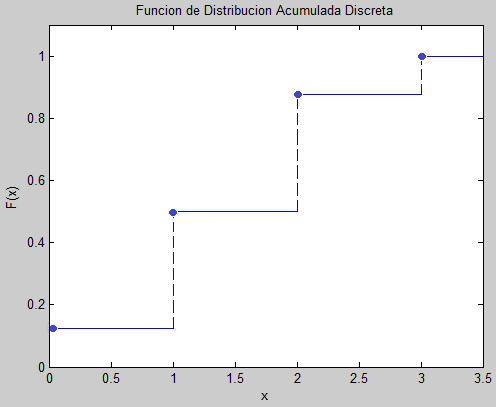
Es momento de practicar con nuestro Ejercicio interactivo de Funcion de Distribución Acumulada de Variables Aleatorias Discretas
| Menú Probabilidad y Estadística | Tema Anterior | Tema Siguiente |