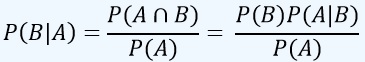

| Menú Probabilidad y Estadística | Tema Anterior | Tema Siguiente |
A menudo se conocen las probabilidades de ciertos eventos condicionados en otros eventos, pero se necesita saber es el evento "inverso". Esto es, dado que se conoce P(A|B), se quiere conocer P(B|A).
En muchos problemas prácticos en la industria, se utiliza la Regla de Bayes para encontrar al "culpable" de una falla en un proceso en el cual se tienen varios "actores", por ejemplo si un producto se produce en cualquiera de varias máquinas, y resulta uno defectuoso, permite hallar cuál es la máquina más probable que provocó la falla.
La regla de Bayes es una sencilla fórmula matemática para calcular P(B|A) cuando se conoce P(A|B). Se basa en el sencillo hecho de que (A∩B) = (B∩A). De esta forma según la probabilidad condicional,
P(A∩B) = P(A)P(B|A). Ec. 1
Así mismo,P(B∩A) = P(B)P(A|B). Ec.2
Pero resulta queP(A∩B) = P(B∩A). Ec. 3
Luego al despejar P(B|A) de la Ec. 1 y sustituir P(B∩A) de la ec. 2 aprovechando la euivalencia dada en la Ec. 3, se obtiene que
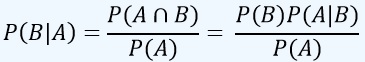
De esta forma y para una partición, se puede llegar a la Regla de Bayes.
Regla de Bayes.Si los eventos B1, B2,..., Bn constituyen una partición de un espacio muestral S, en que P(Bi) ≠ 0 para i=1, 2, ...,n, entonces para cualquier evento A en S, tal que P(A) ≠ 0,
|
Ejemplo: Con referencia al ejemplo anterior, si se presentó un accidente, ¿Cuál es la probabilidad de que haya sido en un dia nuboso?
Solución. El planteamiento de la regla de Bayes para el problema es:
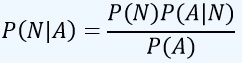
Al sustituir los valores de las probabilidades dados en el problema, se tiene

De la misma forma, para evaluar la probabilidad de que se haya presentado el accidente en un día seco
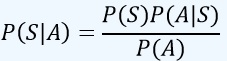
y al sustituir los valores de las probabilidades dados en el problema

Observe que P(S/A) = 1 − P(N/A), ya que solamente se presentan estas dos condiciones en que la particion del espacio muestral tiene los dos eventos de dia Seco (S) o día Nublado (N).
Ahora practique los conceptos con nuestra Aplicación Teorema Probabilidad Total y Regla de Bayes
luego evalúese con el Quiz I Interactivo del Teorema Probabilidad Total y Regla de Bayes
y también evalúese con el Quiz II Interactivo del Teorema Probabilidad Total y Regla de Bayes
| Menú Probabilidad y Estadística | Tema Anterior | Tema Siguiente |