
PROBABILIDAD: TECNICAS DE CONTEO PARTE I
Ya que muchos (no todos) los problemas de Probabilidad se pueden resolver mediante el conteo de los resultados de un Experimento aleatorio, se desarrollarán en esta seccion varios principios de conteo que son de gran utilidad para solucionar problemas de probabilidad
La siguiente definición usa el concepto de conjunto para referirse a todos los resultados posibles de un experimento de probabilidad.
La probabilidad mide el elemento de aleatoriedad que se encuentra asociado a la ocurrencia de determinados eventos. El objetivo inicialmente es contar los distintos arreglos de los puntos en un espacio muestral sin que se tenga que anotar cada uno de ellos.
Por ejemplo, miremos qué pasa cuando se lanza una moneda. Qué puedo obtener al lanzarla, solamente cara o sello , no hay más
opciones en esa moneda. Cuando se trata de contar las posibilidades en una moneda....fácil,
pero y si es algo más complicado que una moneda..... ?
Supongamos que la señora que nos hace el favor de vendernos el almuercito solamente sabe cocinar 4 tipos de sopas (sopa con verduras, de pasta, de arroz y de plátano), además sólo sabe hacer 3 tipos de platos fuertes
(con frijoles, con lentejas y con verduras), sabe hacer además postre de natas, de guayaba y mielmesabe
y sólo da agua con el almuerzo.
¿QUÉ POSIBILIDADES DE ALMUERZO TENEMOS PARA HOY ?
Entonces las
posibilidades son :
1. sopa de verduras con frijoles, postre de natas y agua
2. sopa de verduras con lentejas, postre de natas y agua
3. sopa de verduras con verduras, postre de natas y agua
4. sopa de pasta con frijoles, postre de natas y agua
5. sopa de pasta con lentejas, postre de natas y agua
6. ...etc., etc,
etc...
Alguno dirá : ¡Cambie de restaurante ! (tiene razón)... y otros
observarán todas las posibles variaciones que se pueden generar aún siendo tan
pequeño el menú, sólo enunciamos 5 de 36 posibilidades para el almuerzo de hoy.
Por lo tanto, no es fácil hacer el conteo para todas esas variaciones y más si
se hace una por una. Por ello existen técnicas que sin duda facilitan
notablemente los conteos de todas las posibilidades existentes.
13. Técnicas de Conteo
13.1 Listas
Una lista es una sucesión ordenada de objetos, se escriben entre paréntesis y
separando los elementos por comas. Por ejemplo la lista (1,2,3,Ζ)
es una lista cuyo primer elemento es el 1, el segundo el 2, el tercer elemento
es el 3 y el cuarto elemento es el conjunto de los números enteros.
El orden en que aparecen los elementos en una
lista es de suma importancia, así la lista (2,4,6) es diferente de la lista
(6,4,2) y de la lista (4,2,6) sin importar que los elementos sean los mismos.
Los elementos en una lista pueden repetirse como
en (2,2,3).
La longitud de una lista es la cantidad de
elementos que tiene la lista, así en todos los ejemplos anteriores la longitud
es de tres, mientras que la lista (2,4,6,8) tiene una longitud de cuatro.
Una lista de longitud dos tiene el nombre
especial de par ordenado.
Una lista de longitud cero se llama lista
vacía y se representa por un paréntesis sin elementos en él: ( ).
Con frecuencia las coordenadas de un punto en un
plano se especifican mediante un par ordenado de números reales (x,y).
13.2 Conteo de listas de dos elementos o par ordenado.
Ejemplo. Se desea hacer una lista de dos elementos, en los lugares de la
lista pueden estar cualquiera de los dígitos 2, 4, 6 o 8. ¿Cuántas listas con
estas características son posibles?. La forma más directa de responder es
escribiendo todas las posibilidades:
| (2,2) |
(2,4) |
(2,6) |
(2,8) |
| (4,2) |
(4,4) |
(4,6) |
(4,8) |
| (6,2) |
(6,4) |
(6,6) |
(6,8) |
| (8,2) |
(8,4) |
(8,6) |
(8,8) |
Hay 16 listas posibles.
Se organizan las listas de manera que estemos
seguros de que no hemos repetido ni olvidado alguna. El primer renglón de la
tabla contiene todas las listas posibles que comienzan con 2, el segundo las que
comienzan con cuatro y así sucesivamente. Vemos que como el segundo elemento de
cada lista corresponde a la columna, entonces la primera columna comienza con el
primer elemento que es el 2, la segunda columna con el cuatro y así
sucesivamente. Por todo lo anterior hay 4 filas y cuatro columnas o 4x4 = 16
listas posibles con los cuatro dígitos 2, 4, 6 y 8.
Vamos a generalizar más este ejemplo. Se desea
conocer la cantidad de listas posibles de dos elementos donde haya n
elecciones posibles para cada elemento de la lista. Ahora supongamos que los
elementos posibles son los enteros pares desde el 2 al n. Igual que antes,
organizamos todas las listas posibles en una tabla:
| (2,2) |
(2,4) |
(2,6) ... |
(2,n) |
| (4,2) |
(4,4) |
(4,6) ... |
(4,n) |
| (6,2) |
(6,4) |
(6,6) ... |
(6,n) |
| . |
. |
. |
. |
| : |
: |
: |
: |
| (n,2) |
(n,4) |
(n,6) ... |
(n,n) |
La primera fila contiene todas las listas que
comienzan con 2, la segunda fila las listas que comienzan con 4 y así
sucesivamente. Hay en total n filas y n columnas, ya que para renglón o fila hay
n listas. Por consiguiente hay n x n= n2 listas posibles.
Ahora veamos el caso en que la cantidad de
entradas (opciones) para la segunda posición es diferente de las opciones para
la primera. Por ejemplo imagine que una comida es una lista de dos elementos,
formada por una entrada (o plato principal) y el postre. La cantidad de postres
podría ser diferente a la de las entradas posibles.
De esta forma nos preguntamos ahora ¿cuántas
listas son posibles de dos elementos en las que haya n opciones para el primer
elemento y m opciones para el segundo?. Supongamos que los elementos posibles en
la primera posición de la lista son los enteros del 1 al n y los posibles para
la segunda posición son los enteros del 1 al m. Como antes tenemos la siguiente
tabla con las diferentes posibilidades:
| (1,1) |
(1,2) |
(1,3) ... |
(1,m) |
| (2,1) |
(2,2) |
(2,3) ... |
(2,m) |
| (3,1) |
(3,2) |
(3,3) ... |
(3,m) |
| . |
. |
. |
. |
| : |
: |
: |
: |
| (n,1) |
(n,2) |
(n,3) ... |
(n,m) |
Hay n filas o renglones (con el primer elemento
igual en cada una de las listas), y cada fila contiene m listas. Por
consiguiente la cantidad de listas posibles es:
|
m + m + m +...+ m |
= m X n |
|
n veces |
|
| Definición 13.1 Principio de Multiplicación: Consideremos listas
de dos elementos en las que hay n
opciones para la primera posición, y cada opción del primer elemento tiene
m opciones para el segundo elemento.
Entonces la cantidad de estas listas es de nm. |
| Ejemplo 1:
Las iniciales de una persona (suponiendo que sólo nos interesa el primer
nombre así tenga segundo nombre) son las listas formadas por las iniciales
de su nombre y su apellido (primer apellido). Por ejemplo las iniciales del
autor son WC.
a. ¿De cuántas formas se pueden escribir las iniciales de las personas?
b. ¿De cuántas formas se pueden escribir las iniciales en las que las dos
letras sean distintas? (Por ejemplo CC de Carmen Cardona no se permitiría).
Para contestar la pregunta y omitiendo la ch (Chavo o Chávez), la Ll por
ser letras dobles y deseamos sólo dos iniciales,y la ñ y con un alfabeto al
estilo inglés de 26 letras tendremos estos 26 elementos para la primera
posición de cada lista y así mismo 26 opciones para la segunda posición,
luego hay 262 = 676 listas posibles (o en el caso de
considerar la ñ 272 =729 listas posibles).
b. La segunda pregunta pide la cantidad de listas de dos elementos,
habiendo 26 opciones para el primer elemento (n=26) y para cada una de
ellas, 25 opciones para el segundo (m=25). Por consiguiente hay 26 x 25
listas (nm listas posibles).
|
| Ejemplo 2: Un club tiene 15 miembros. Desean elegir un
presidente y alguien más como vicepresidente. ¿De cuántas formas pueden
llenarse esos cargos?
Al reformular la pregunta como una de conteo de listas, tenemos: ¿Cuántas
listas de dos elementos se pueden formar en las que dos elementos sean
personas seleccionadas de un total de 15 candidatos y que la misma persona
no se seleccione dos veces (no esté repetida)?.
hay 15 opciones para el primer elemento de la lista (primera posición,
n=15) y para cada una de estas (para cada presidente) hay 14 opciones (m=14)
para el segundo elemento de la lista (el vicepresidente). Según el principio
de la multiplicación, hay 15 X 14 (nm) posibilidades. |
13.4 Listas de más de dos elementos.
El principio de la multiplicación se puede aplicar a listas más largas.
Pensemos en las listas de tres elementos o longitud tres. Supongamos que hay a
opciones para el primer elemento, para cada uno de estos hay b opciones para el
segundo elemento y para cada opción del par formado por el primer y segundo
elemento hay c opciones para el tercer elemento. De esta forma hay en total abc
listas posibles.
Una forma provechosa de imaginar problemas de conteo de listas es hacer una
diagrama con cuadros. Cada cuadro representa una posición en la lista.
Escribimos la cantidad de elementos posibles en cada cuadro. El total de listas
posibles se calcula multiplicando entre sí esas cantidades.
Ejemplo 3:Hay un club con 15 socios. Se desea elegir una
mesa directiva formada por un presidente, un vicepresidente, un secretario y
un tesorero. ¿De cuántas maneras se puede hacer la elección, suponiendo que
un socio puede ocupar sólo un cargo?. Trazamos el siguiente diagrama:
Esto nos muestra que hay 15 socios para elegir el presidente. Una vez
seleccionado el presidente quedan 14 socios para ser elegidos como
vicepresidente y en consecuencia hay 15 X 14 formas de elegir al presidente
y al vicepresidente. Una vez elegidos, hay 13 formas de elegir al tercer
elemento (el secretario). Una vez elegidos los tres primeros cargos quedarán
12 socios para elegir entre estos al tesorero. En consecuencia hay 15 X 14 X
13 X 12 formas de seleccionar la mesa directiva. |
14. Principio Fundamental de Conteo
Si un suceso A presenta n1
maneras diferentes y una
vez este suceso ha ocurrido un segundo suceso B se puede presentar en n2
maneras diferentes y así
cuando ha ocurrido este, sucede un tercer suceso C que se puede presentar
en n3 maneras diferentes
y así diferentes sucesos en nk formas, entonces el número total de maneras
diferentes como pueden darse simultáneamente los sucesos es :
n1*n2*n3*........*nk
Volviendo al ejemplo inicial de los almuerzos, entonces los posibles menús con sus 4 sopas, 3 platos fuertes, 3 postres y agua
se hubiesen podido contar más fácilmente así :
4*3*3*1=36 posibles menús.También es importante en probabilidad
familiarizarse con otras terminologías como las variaciones que veremos a
continuación:
15. Variaciones sin repetición
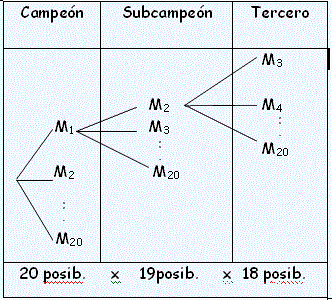
En una carrera de
carros participan 20 corredores. Teniendo en cuenta que no es posible llegar la
mismo tiempo , ¿ de cuantas maneras podrán llegar a la meta los tres primeros?
Elegimos una notación adecuada , por ejemplo m1,m2...m20, para representar a los
20 corredores.
Para la primera posición (campeón) hay 20 posibilidades; para la segunda
posición (subcampeón) hay 19 posibilidades , y para el tercer puesto hay 18
posibilidades.
Observamos el diagrama de árbol del margen.
Por tanto, hay 20,19.18=6840 formas distintas de quedar los tres primeros
clasificados .
A estos distintos grupos ordenados de tres corredores , elegidos de entre los 20
que tenemos, lo llamaremos variaciones de 20 elementos tomando de a tres cada
vez.
Variaciones ordinarias o variaciones
sin repetición de n elementos tomados m cada vez (m ≤
n) son
los distintos grupos o listas que se pueden formar con los n
elementos, de manera que:
- En cada grupo entren m elementos, distintos
- Dos grupos son distintos si se diferencian en algún elemento o en el orden de
colocación de éstos .
El número de variaciones ordinarias de n elementos tomando m
cada vez se representa por Vn,m
|
Número de variaciones ordinarias
Hemos obtenido el número de formas de clasificarse 20 corredores para obtener
los tres primeros puestos: 20x19x18.
En general, si hallamos el número de variaciones sin repetición que se pueden
formar con n elementos tomados m a m, obtendremos:
| Vn,m = |
| n |
(n-1) |
(n-2) |
... |
(n-m+1) |
|
Ejercicios resueltos:
ATENCIÓN A QUE:
Vn,0 no tiene sentido
Vn,1= n
Vn,2 = n(n-1)(n-2)
Vn,3 = n(n-1)(n-2)(n-3)
Vn,n = n(n-1)(n-2)(n-3) ...3·2·1.
Así por ejemplo:
V3,2= 3·2
= 6que podría ser un grupo de tres socios, por ejemplo Alejandra (A), Carlos
(C) y Wilson (W) entre los cuales se van a designar dos cargos importantes:
Representante Legal y tesorero. Si la primera posición es para el Representante
legal y la segunda para el tesorero tenemos las siguientes posibilidades:
|
(A,C), (A,W)
(C,A), (C,W)
(W,A),(W,C) |
Para este caso siempre quedaría uno de ellos sin un cargo, porque son 3
elementos (n=3) tomados 2 cada vez (m=2).
Si todos quieren quedar con un cargo, digamos ahora que entre los 3 socios
(n=3) se van a elegir como Presidente de la Mesa directiva y los cargos de
Representante Legal y tesorero. En este caso tenemos V3,3 así:
V3,3 = 3·2·1=6 también 6 posibilidades, pero
ahora tenemos:
|
(A,C,W), (A,W,C)
(C,A,W), (C,W,A)
(W,A,C), (W,C,A |
y así cada uno de los socios tiene un cargo y
estarán felices.
1. Resolver la ecuación Vn,4 = 20Vn,2
Como Vn,4 = n(n-1)(n-2)(n-3) y = Vn,2 = n(n-1)
y m ≥ 4, sustituyendo tenemos:
| n(n-1)(n-2)(n-3) = 20n(n-1)
(n-2)(n-3) = 20
n=7 |
2. ¿Cuántos números de tres cifras se pueden formar con los dígitos 1,2, 3,
4, 5, 6, 7, 8 y 9 sin que se repita ninguna cifra?
Como el número 123 es diferente del número 321, luego influye el orden y
además no se puede repetir ninguna cifra. Por lo tanto debemos calcular el
número de variaciones de nueve elementos (n=9) tomando tres cada vez (m=3):
V9,3 = 9·8·7 = 504
números distintos.
3. Se quiere cambiar la bandera
de una ciudad de tal forma que esté formada por tres franjas horizontales de
igual ancho y distinto color. ¿Cuántas banderas distintas se podrán formar con
los siete colores del arco iris?
Como influye el orden en que se
establezcan los colores y además no se puede repetir ningún color, tendremos que
calcular el número de variaciones ordinarias de siete elementos (n=7) tomando
tres cada vez:
V7,3 = 7·6·...(7-3+1)
= 7·6·5 = 210 banderas distintas
Ya necesitaríamos a un buen
diseñador gráfico para que nos muestre las mejores combinaciones de colores de
las banderas ganadoras.
4. ¿De cuántas maneras distintas
se pueden sentar 12 alumnos en los cuatro asientos de la primera fila de la
clase? ¿Y si el primer asiento está siempre reservado para el delegado del
curso?
Para el primer caso debemos
calcular el número de variaciones de 12 elementos (n=12) tomados de a cuatro
cada vez (m = 4):
V12,4 =
12·11·...(12-4+1) = 12·11·10·9 = 11880 formas distintas.
En el segundo caso como hay un
estudiante menos (n=11) en el juego de posibilidades (el delegado siempre va a
estar en el primer asiento) y un asiento menos (m=3), luego vamos a calcular el
número de variaciones de 11 elementos tomados de a tres:
V11,3 =
11·10·...(11-3+1) = 11·10·9 = 990 formas distintas.
16. Variaciones con Repetición
Lanzamos cuatro veces
consecutivas una moneda obteniendo en cada caso una Cara (C) o Cruz (X). Cuántos
resultados distintos podremos obtener?
Formemos el diagrama de árbol correspondiente:
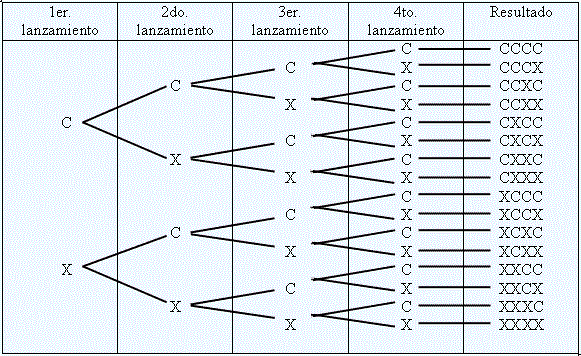
Las distintas ordenaciones que acabamos de obtener se llaman
variaciones con repetición de dos elementos tomados de a cuatro cada vez.
Observamos que ahora sigue influyendo el orden, como en el
caso anterior, pero además los elementos se pueden repetir:
Definición 16.1 Variaciones con repetición de n elementos tomados
m cada vez (m ≤ n) son
los distintos grupos o listas que se pueden formar con los n
elementos, de manera que:
- En cada grupo entren m elementos, repetidos o no.
- Dos grupos son distintos si se diferencian en algún elemento o en el orden de
colocación de éstos .
El número de variaciones con repetición de n elementos tomando m
cada vez se representa por VRn,m. |
Número de Variaciones con Repetición.
Hemos hallado el número de resultados distintos que se
obtienen al lanzar cuatro veces una moneda: 2 · 2 ·
2 · 2 = 24 = 16
De la misma forma, podemos
hallar el número de resultados distintos que se obtienen al lanzar:
- Una vez una moneda: 2.
- Dos veces una moneda: 2 · 2 =
22 = 4 (¿Cuáles son estas posibilidades?)
- Tres veces una moneda: 2 · 2 ·
2 = 23 = 8
- Cinco veces una moneda: 2 · 2
· 2 · 2 = 25.= 32
- Ene (n) veces una moneda: 2 ·
2 · 2... · 2 = 2n.
En general si queremos hallar el
número de variaciones con repetición que se pueden formar con n elementos
tomados de a m cada vez, obtendremos:
| VRn,m = n · n · n ·... n = nm
|
|
m factores |
|
.Ejercicios
1. Resolver VRx,2 +
5VRx-2, 2 = 224
Como VRx,2 = x2
y VRx-2, 2 = (x-2)2 , sustituyendo:
x2 + 5 (x-2)2
= 244
x2 + 5 (x2-4x
+ 4) = 244
x2 + 5x2-20x
+ 20 = 244
6x2 - 20x - 224
= 0 , resolviendo la ecuación cuadrática
x = 8 o X = -14/3
La solución válida es x=8 ya que
la otra solución carece de sentido.
| 2. En el alfabeto Morse se
utilizan dos símbolos: el punto y la raya. ¿Cuántos caracteres diferentes es
posible obtener en el citado alfabeto tomando 1, 2, 3 o 4 de los símbolos citados?
Caracteres formados por un sólo símbolo:
VR2,1 = 2
Caracteres formados por dos símbolos:
VR2,2 = 22 = 4
Caracteres formados por tres símbolos:
VR2,3 = 23 = 8
Caracteres formados por cuatro
símbolos: VR2,4 = 24 = 16
Total de caracteres diferentes: S = 2 + 4 +
8 + 16 = 30
|
|
A . _
B _ . . .
C _ .
_ .
D _ . .
|
N _ .
O _ _ _
P . _ _ .
Q _ _ . _ |
| |
E .
F . . _ .
G _ _ .
H . . . . |
R . _ .
S ...
T _
U .
. _ |
| |
I . .
J . _ _ _
K _ . _
L
. _ . . |
V . . . _
W . _ _
X _ .
. _
Y _ . _ _ |
| |
M _ _
1 . _ _ _ _
2 . . _ _ _
3 . . . _ _ |
Z _ _ . .
6 _ . . . .
7 _ _
. . .
8 _ _ _ . . |
| |
4 . . . . _
5 . . . . |
9 _ _ _ _ .
0 _ _ _ _ _ |
3. ¿Cuántos números de tres cifras se pueden formar con los
dígitos 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 si se pueden repetir las cifras?
Tenemos que hallar el número de variaciones con repetición de
10 elementos tomados de a tres, es decir:
VR10,3 = 103 = 1000
Ahora bien, de estos 1000 números habrá muchos que inicien
con cero como por ejemplo 035, 099, 001 por lo cual no se pueden considerar de
tres cifras. Por esto debemos descontar estos números, y tendremos:
VR10,3 - VR10,2 = 103 - 102
= 1000 - 100 = 900
4. Se lanzan tres dados de distintos colores una vez.
¿Cuántos resultados distintos se pueden obtener?
Son VR6,3 = 63 = 216 resultados
diferentes.
Algunas veces queremos saber cuántos arreglos podemos obtener con un grupo de
elementos, para ello podemos utilizar la técnica conocida como permutación que
veremos a continuación en el siguiente tema.


