
| Menú Probabilidad y Estadística | Tema Anterior | Tema Siguiente |
La probabilidad mide el elemento de aleatoriedad que se encuentra asociado a la ocurrencia de determinados eventos. El objetivo inicialmente es contar los distintos arreglos de los puntos en un espacio muestral sin que se tenga que anotar cada uno de ellos.
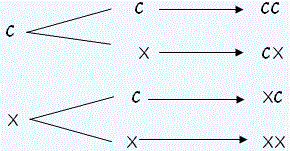
2. El experimento consiste en lanzar dos monedad sobre una mesa y anotar los resultados de las caras superiores tiene por espacio muestral el siguiente:
| E = {CC,CX, XC,XX} |
 |
| Una forma sencilla de obtener en estos casos el espacio muestral es mediante un diagrama de árbol , como se indica a la derecha. |
3. Experimento: Observar el número de veces que se requiere lanzar una moneda hasta obtener por primera vez un "sello" (X). Aquí:
S = {1, 2, 3, ..., ∞}
tenga en cuenta que el punto muestral "1" indica que se obtuvo "sello" en el primer lanzamiento de la moneda, así como "3" indica que los dos primeros lanzamientos se obtuvo "cara". El punto muestral "∞" indica que nunca se obtuvo "sello".
Al analizar el Experimento aleatorio: Lanzamiento de un dado corriente tres veces consecutivas, se tiene que los posibles resultados son triplas de la forma (a, b, c), con cada a, b, c ∈ {1, 2, 3, 4, 5, 6}. Esto es:
S = {(a, b, c): a, b, c ∈ {1, 2, 3, 4, 5, 6}}
Se podría construir un diagrama de árbol para especificar los posibles arreglos que describe S. Luego se verán algunas técnicas para hallar estos arreglos.
Sea el evento: "La suma de resultados obtenidos es mayor o igual que 14", esto es:
A: = {(a,b,c) ∈ S: a + b + c ≥ 14}
A: = {(5,5,4),(4,5,5),(5,4,5),(5,5,5),(6,5,5),(5,6,5),(5,5,6),(6,6,5),(6,5,6),(5,6,6),(6,6,6}
Definición 5.3. Evento o Suceso. Un evento o suceso A (respecto a un espacio muestral S), es un subconjunto de elementos de S. En particular ∅ se denomina el evento imposible y S el evento seguro. Los eventos con un solo elemento se denominan eventos elementales. |
Ejemplo 3. Experimento aleatorio: lanzar un dado cuyas caras están numeradas del 1 al 6
El espacio muestral del experimento es :
S = {1,2,3,4,5,6}
Consideremos ahora algunos subconjuntos de S; por ejemplo:
Salir par: A = {2,4,6}
Salir impar: B = {1,3,5}
Salir múltiplo de 3: C = {3,6}
Observamos que todos estos subconjuntos de S son eventos (o sucesos)
Ejercicios resueltos
1.Determinar el espacio muestral y el espacio de sucesos del experimento
aleatorio que consiste en lanzar una moneda y anotar el resultado de la cara
superior.
Espacio muestral: E = {C,X}
Espacio de sucesos S = {Ø,{C},{X},{C,X}}
Cuando nos referimos a eventos en lenguaje común, a menudo los negamos (el resultado no es un número PAR) o los combinamos usando las palabras "y" u "o" (el resultado es un número PAR y PRIMO). La teoría de conjuntos tiene una notación conveniente para usar con dichos eventos compuestos.
Eventos compuestos:
Se llama eventos compuestos, a los formados por dos o más puntos muestrales; es decir, por mas de un resultado del experimento. Así los eventos A ∪ B, A ∩ B, para el evento unión ("o") y evento intersección ( "y"), respectivamente.
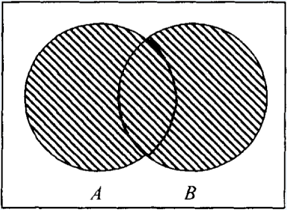
| A ∪ B | A ∩ B |
 |
 |
| Dados dos eventos A y B de un mismo experimento aleatorio, llamamos evento unión de A y B al suceso que se realiza cuando se realiza A o B y se representa por A ∪ B. El evento A ∪ B esta formado por los puntos muestrales de A y de B. |
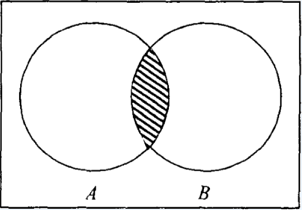
| Dados dos eventos A y B de un mismo experimento aleatorio ,
llamaremos evento de intersección de A y B al suceso que se realiza
cuando se realizan simultáneamente los eventos A y B.
El evento A intersección B se representa por A ∩ B, también A y B. El suceso A ∩B esta formado por los puntos muestrales comunes a los sucesos A y B. |
Eventos contrarios:
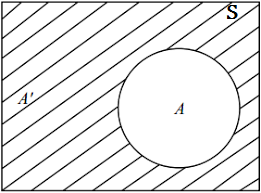
Consideremos los eventos A y Ac (también se simboliza con A′, ∼A, o Ā ), para el evento complemento , contrario o negación de A.
Ejemplo. Consideremos el espacio muestral asociado al lanzamiento del dado,| Dado un evento cualquiera A del espacio de eventos S, se llama evento contrario de A a un evento Ac que ocurre cuando no se realiza A, y recíprocamente. |
Ahora vamos a ver ejemplos con estas operaciones dada su importancia en el estudio de la Probabilidad. Luego podrá practicar con cuestionarios interactivos.
- Unión de sucesos
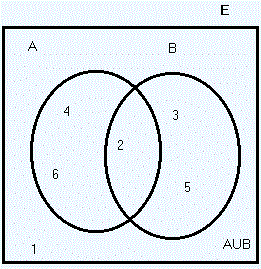 |
A ∪ B={2,3,4,5,6}
Consideremos , en el experimento aleatorio del lanzamiento del dado, cuyo espacio muestral es
|
Intersección de eventos Consideremos nuevamente los sucesos A y B del ejemplo anterior: D = A ∩ B = {2} Y se llama evento de intersección de A y B. |
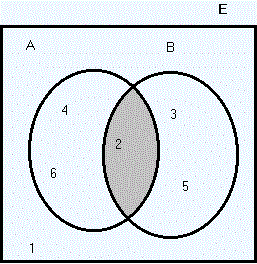 |
| A ∩ B |
La Ley distributiva para números reales es
a(b + c) = ab + ac
Dos leyes distributivas similares para conjuntos y por consiguiente para operaciones con eventos, son las siguientes:
A ∩ ( B∪ C) = (A ∩ B) ∪ ( A ∩ C) A ∪ ( B∩ C) = (A ∪ B) ∩ ( A ∪ C) |
Estas leyes son útiles para tratar eventos compuestos que incluyan los conectores lógicos Y (∧) y O (∨). Estas leyes nos dicen que
A y (B o C) es equivalente a (A y B) o (A y C)
y que
A o (B y C) es equivalente a (A o B) y (A o C)
Ejemplo. Una compañía de servicios financieros está estudiando un grupo de individuos que son clientes potenciales. La compañía ofrece vender acciones, bonos y seguros de vida a sus clientes. Los eventos de interés son los siguientes:
A: el individuo posee acciones
B: el individuo posee bonos
C: el individuo tiene cobertura de seguro de vida.
Las leyes distributivas nos dicen que
A ∩ ( B∪ C) = (A ∩ B) ∪ ( A ∩ C)
A ∪ ( B∩ C) = (A ∪ B) ∩ ( A ∪ C)
La primera identidad establece que:
(Poseer Acciones) y (poseer bonos o estar asegurado) es equivalente a (poseer acciones y poseer bonos) o (poseer acciones y estar asegurado)
Ejercicio. Interprete la segunda identidad.
Dos relaciones muy útiles, son las siguientes:
i) ( A∪ B)c = Ac ∩ Bc ii) ( A∩ B)c = Ac ∪ Bc |
Una forma equivalente y alternativa de las Leyes de Morgan con la negación de un evento A como ∼ A, son:
i) ∼( A∪ B) = ∼ A ∩ ∼ B ii) ∼( A∩ B) = ∼A ∪ ∼B |
Que establecen que
no(A o B) es equivalente a (no A) y (no B)
y que
no(A y B) es equivalente a (no A) o (no B)
Ejemplo. Con los eventos A (poseer acciones) y B (poseer bonos) del ejemplo anterior. Las leyes de De Morgan establecen que
i) ∼( A∪ B) = ∼ A ∩ ∼ B, y
ii) ∼( A∩ B) = ∼A ∪ ∼B
que en palabras se interpreta la primera identidad como:
no(poseer acciones o poseer bonos) es equivalente a (no poseer acciones) y (no poseer bonos)
Ejercicio. Interprete en palabras la segunda identidad.
10. Eventos IncompatiblesEn los ejemplos anteriores hemos visto que en algunas ocasiones la intersección de dos eventos es el suceso imposible. Cuando esto ocurre, es decir, cuando es imposible que dos eventos se realicen simultáneamente , decimos que dichos eventos son incompatibles.Es decir, datos dos eventos Ay B de un mismo experimento aleatorio, se tiene que: |
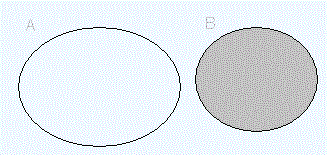
Eventos incompatibles |
|
Obsérvese que un evento y su contrario son incompatibles |
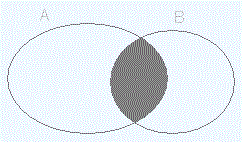
Eventos compatibles |
|
| Es fácil observar que estos eventos cumplen las siguientes
propiedades : 1. A U B U C = S 2. A, B,C son incompatibles dos a dos. A un conjunto de eventos que cumpla estas dos condiciones lo llamaremos Sistema completo de eventos o Partición de un espacio muestrals. |
 |
| De una manera general, se dice que los eventos A1, A2, A3..., An constituyen un sistema completo de eventos para un determinado
experimento aleatorio , si se verifica: 1. A1 U A2 U A3 U...U An = S 2. A1, A2, A3..., An son incompatibles dos a dos. |
| E = {(1,C), (2,C), (3,C), (4,C),(5,C), (6C),(1,X), (2,X), (3,X), (4,X),(5,X), (6X)} |
Ya que muchos (no todos) los problemas de Probabilidad se pueden resolver mediante el conteo de los resultados de un Experimento aleatorio, se desarrollarán en la siguiente seccion varios principios de conteo que son de gran utilidad para solucionar problemas de probabilidad
Ejercicios de práctica: Ejercicio 1 Ejercicio 2
| Menú Probabilidad y Estadística | Tema Anterior | Tema Siguiente |