Ejercicio especial de fracciones parciales, realizado por Wilson Castro Z., docente Ciencias Básicas Universidad de San Buenaventura -Bogotá.

Resolver la integral indefinida:

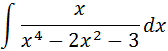
Para el desarrollo de esta integral, se van a realizar dos procedimientos de fracciones parciales, teniendo en cuenta que al factorizar se puede tener:
- Procedimiento A: con solamente caso III (Factores cuadráticos irreducibles), lo cual No es cierto para la diferencia x² − 3 la cual es factorizable pero como se verá más adelante (Procedimiento B) nos genera un sistema de ecuaciones más extenso para hallar los coeficientes de las fracciones. Luego se puede realizar el procedimiento como si fuera un factor cuadrático irreducible, sin factorizar, como se observa en el desarrollo A del mismo. Luego se realizará el procedimiento B factorizando todo lo que se pueda como debería ser.
- Procedimiento B: con los casos I y III

Procedimiento A: caso III (Factores cuadráticos irreducibles)

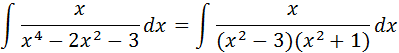
Aplicando fracciones parciales caso III (Factores cuadráticos irreducibles):

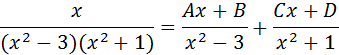
Al simplificar denominadores y desarrollador los factores, se tiene:

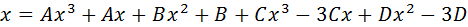
Factorizando las potencias de la variable x:

Al igualar los coeficientes de las potencias de x: , tenemos:

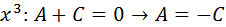
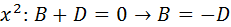
Con lo cual la solución es:

La integral ahora queda como:

Se realizan las siguientes sustituciones:

Con lo cual la primera integral da:

La segunda integral da:

La integral total, aplicando propiedades de logaritmos, es:

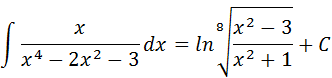
Puede ver la Comprobación en este link

Método II: Factorizando la diferencia de cuadrados

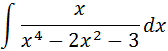
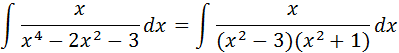
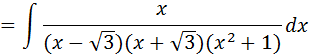
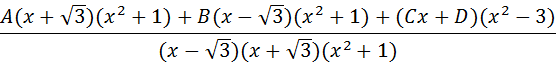
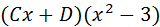
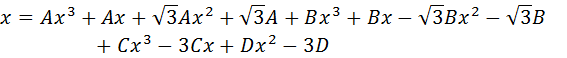
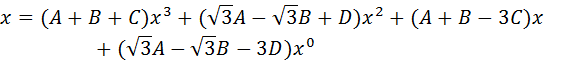
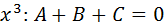
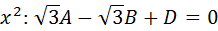
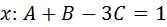
Se puede resolver este sistema de ecuaciones de varias formas, aquí se plantea hallar la solución con Matlab con el código:

format rat
x=[1,1,1,0;sqrt(3),-sqrt(3),0,1;1,1,-3,0;sqrt(3),-sqrt(3),0,-3]
b=[0;0;1;0]
sol=inv(x)*b %Tambien se puede resolver directamente con: x\b
La solución es: A= 1/8, B=1/8, C= -1/4, D= 0

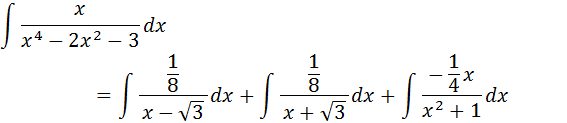
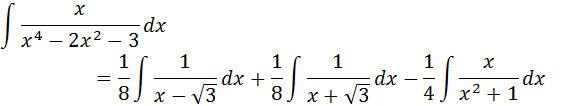
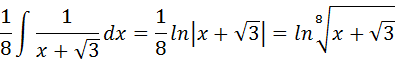
Luego la suma de ambos resultados por las propiedades de los logaritmos, es:

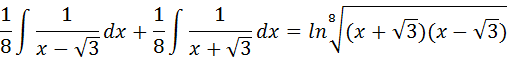
Para la última integral, se realiza la sustitución:

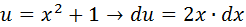
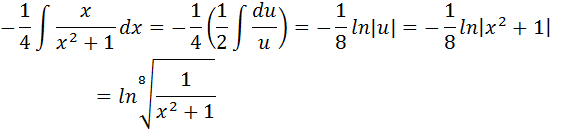
El resultado final, nuevamente combinando los resultados previos con propiedades de los logaritmos, es:

En programas como Matlab el resultado aparece en términos de la arcotangente hiperbólica como: −atanh((2*x^2)/(x^2 + 3))/4

Puede ver la Comprobación en este link