Se Actuario

Integración por partes

Principal Cálculo Anterior Siguiente

La integración por partes proviene de la Regla del producto en la derivación. La fórmula de la Integración por partes es:

∘ El paso clave es decir como escribir la integral como el producto de dos funciones uv'.

∘ Tenga en cuenta que la Integración por partes es útil cuando u'v es más fácil (o al menos no más difícil) de integrar que uv'. Algunas pistas para esto son:

   - Escoja a u de tal forma que u' sea más sencillo que el mismo u.

   - Escoja v' de tal manera que se pueda evaluar su integral:

   - De acuerdo al ejercios, puede ser una buena selección v' = 1

Si la integral está definida, la forma es:

Ahora revise los siguientes ejercicios en los cuales se aplica la técnica de integración por partes:

   
  Integral por partes

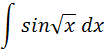Primero se realiza la sustitución: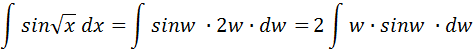

Integral por partes
Integral por partes

Integrando por partes según: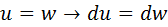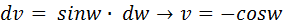

Integral por partes
Integral por partes
Integral por partes
Integral por partes

Y retornando a la variable original, se tiene la solución de la integral: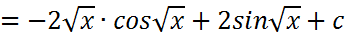

Integral por partes
  
     
   
     
 

12)

MATH

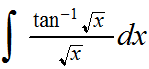
Integrando por partes:

$u=tan^{-1}\sqrt{x}$ → MATH

MATH → $v=2\sqrt{x}$

MATH

Sustitución: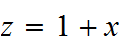

$z=1+x$ → $dz=dx$

MATH


 
     
 

13)

MATH

=MATH

=MATH

Evaluando la 1ra. integral por partes:

$u=x$ →$du=dx$

$dv=\sec ^{2}xdx$ → $v=\tan x$

MATH

MATH

La integral total es:

MATH

 
     
   
     
Principal Cálculo Anterior Siguiente