DISTRIBUCIONES DE PROBABILIDAD CONJUNTA DE VARIABLES CONTINUAS

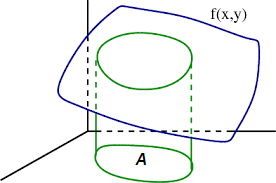
Cuando X e Y son variables aleatorias continuas, las probabilidades se deben encontrar utilizando una función continua de las dos variables o función de densidad conjunta f(x,y) . Esta función de dos variables definirá una superficie de tres dimensiones. La superficie se encuentra sobre el plano x-y, y P[(X,Y)∈ A]. Donde A es una región sobre el plano xy, que es igual al volumen del cilindro recto limitado por la base A y la superficie. Las probabilidades se calcularán como los volúmenes debajo de esta superficie, y se usarán integrales dobles en este cálculo.

Definición. La función f(x,y) es una función de densidad conjunta de las variables aleatorias X y Y si

Ejemplo 1. Una compañía está estudiando la cantidad de bajas por enfermedad (licencias por incapacidad) tomadas por sus empleados. La compañía permite un máximo de 100 horas de licencia por enfermedad pagada en un año. La variable aleatoria X representa el tiempo en horas de incapacidad tomada por un empleado seleccionado al azar el año pasado. La variable aleatoria Y representa el tiempo de licencia tomado por el mismo empleado este año. Cada variable aleatoria se mide en cientos de horas, por ejemplo, X= 0.50 significa que el empleado tomó 50 horas por incapacidad el año pasado. Por lo tanto, X y Y toman valores en el intervalo [0, 1]. La función de densidad de probabilidad conjunta f(x,y) para X e Y es

f(x,y) = 2 − l.2x − 0.8y,    para    0 ≤ x ≤ 1,   0 ≤ y ≤ 1.

La superficie se ilustra en la siguiente figura:

Encuentre: a) Prueba si f(x,y) es una función de densidad.

b) Encuentre P(X ≥ 0.50, Y ≥ 0.50)

Solución. a)Primero se verifica que se trate de una función de densidad:

b) Ahora se evalúa la probabilidad solicitada:

El volumen que representa este cálculo de la probabilidad, se ilustra como:

Distribuciones marginales. Las funciones de densidad marginal de X y Y se definen cuando estas variabes se consideran por separado, es decir, sólo de X y sólo de Y. Estas se definen como:

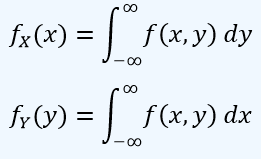
Ejemplo 2. Para las variables aleatorias del ejemplo 1, que tratan del tiempo de incapacidad por enfermedad, las funciones de densidad marginales son:

para sólo X. Para sólo Y es:

Probabilidad condicional

Para la probabilidad condicional se usan los mismos conceptos que en el caso discreto. Para el caso continuo se debe encontrarla función f(x|y) o f(y|x) para integrarla.

Ejemplo 3. Probabilidad Condicional

Para el caso del ejemplo 1, calcule la probabilidad de que un trabajador se incapacite más de 70 horas este año si se incapacitó 60 horas el año pasado.

Se pide hallar P(Y ≥ 0.7|X = 0.6)

La función f(y|x) se establece como

Luego para X = 0.6 se simplifica a:

La probabilidad solicitada es: