 |

| Menú Probabilidad y Estadística | Tema Anterior | Tema Siguiente |
Asimetría
La asimetría se refiere a si la curva que forman los valores de la serie presenta la misma forma a izquierda y derecha de un
valor central (media aritmética). La moda siempre se corresponde con el valor máximo de la curva, mientras que la media o
promedio se ve afectada por los valores extremos. Así, si la curva tiene asimetría negativa (o lo mismo, es asimétrica negativa), la media
se va a desplazar hacia la izquierda en que se presentan una mayor cantidad de valores menores. La mediana estará en ambos casos de asimetría en un punto intermedio de la media y
la moda.
 |
Se observa así mismo que según el tipo de simetría, las medidas de tendencia central tienen las características:
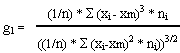 |
Los resultados pueden ser los siguientes:
g1 = 0 (distribución simétrica; existe la misma concentración de valores a la derecha y a la izquierda de la media).
g1 > 0 (distribución asimétrica positiva; existe mayor concentración de valores a la derecha de la media que a su izquierda)
g1 < 0 (distribución asimétrica negativa; existe mayor concentración de valores a la izquierda de la media que a su derecha).
|
Variable
|
Frecuencias
absolutas
|
Frecuencias
relativas
|
||
|
(Valor)
|
Simple
|
Acumulada
|
Simple
|
Acumulada
|
|
1,20
|
1 |
1
|
3,3%
|
3,3%
|
|
1,21
|
4
|
5
|
13,3%
|
16,6%
|
|
1,22
|
4
|
9
|
13,3%
|
30,0%
|
|
1,23
|
2
|
11
|
6,6%
|
36,6%
|
|
1,24
|
1
|
12
|
3,3%
|
40,0%
|
|
1,25
|
2
|
14
|
6,6%
|
46,6%
|
|
1,26
|
3
|
17
|
10,0%
|
56,6%
|
|
1,27
|
3
|
20
|
10,0%
|
66,6%
|
|
1,28
|
4
|
24
|
13,3%
|
80,0%
|
|
1,29
|
3
|
27
|
10,0%
|
90,0%
|
|
1,30
|
3
|
30
|
10,0%
|
100,0%
|
Recordemos que la media de esta muestra es 1,253
| S((xi - x)^3)*ni | S((xi - x)^2)*ni |
|
0,000110
|
0,030467
|
Luego:
Por lo tanto el Coeficiente de Fisher de Simetría de esta muestra es -0,1586,
lo que quiere decir que presenta una distribución asimétrica negativa (se
concentran más valores a la izquierda de la media que a su derecha).
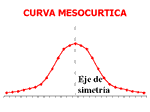
-Distribución mesocúrtica: presenta un grado de concentración medio alrededor de los valores centrales de la variable (el mismo que presenta una distribución normal).
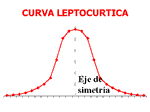
-Distribución leptocúrtica: presenta un elevado grado de concentración alrededor de los valores centrales de la variable.
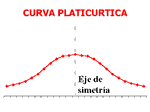
-Distribución platicúrtica: presenta un reducido grado de concentración alrededor de los valores centrales de la variable.
 |
 |
 |
El Coeficiente de Curtosis viene definido por la siguiente fórmula:
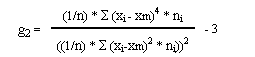 |
Los resultados pueden ser los siguientes:
g2 = 0 (distribución mesocúrtica).
g2 > 0 (distribución leptocúrtica).
g2 < 0 (distribución platicúrtica).
Ejemplo: Vamos a calcular el Coeficiente de Curtosis de la serie de datos referidos a la estatura de un grupo de alumnos (lección 2ª):
|
Variable
|
Frecuencias
absolutas
|
Frecuencias
relativas
|
||
|
(Valor)
|
Simple
|
Acumulada
|
Simple
|
Acumulada
|
|
1,20
|
1 |
1
|
3,3%
|
3,3%
|
|
1,21
|
4
|
5
|
13,3%
|
16,6%
|
|
1,22
|
4
|
9
|
13,3%
|
30,0%
|
|
1,23
|
2
|
11
|
6,6%
|
36,6%
|
|
1,24
|
1
|
12
|
3,3%
|
40,0%
|
|
1,25
|
2
|
14
|
6,6%
|
46,6%
|
|
1,26
|
3
|
17
|
10,0%
|
56,6%
|
|
1,27
|
3
|
20
|
10,0%
|
66,6%
|
|
1,28
|
4
|
24
|
13,3%
|
80,0%
|
|
1,29
|
3
|
27
|
10,0%
|
90,0%
|
|
1,30
|
3
|
30
|
10,0%
|
100,0%
|
Recordemos que la media de esta muestra es 1,253.
| S((xi - xm)^4)*ni | S((xi - xm)^2)*ni |
|
0,00004967 |
0,03046667 |
Luego:
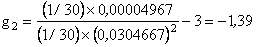 |
Por lo tanto, el Coeficiente de Curtosis de esta muestra es -1,39, lo que quiere decir que se trata de una distribución platicúrtica, es decir, con una reducida concentración alrededor de los valores centrales de la distribución
Ahora practique En EXCEL el Cálculo mediante tres métodos distintos con la Guía de VARIANZA, COEFICIENTE DE ASIMETRIA Y CURTOSIS