
| Menú Probabilidad y Estadística | Tema Anterior | Tema Siguiente |
Si los valores que toma la variable son muy diversos y cada uno de ellos se repite muy pocas veces, entonces conviene agruparlos por intervalos, ya que de otra manera obtendríamos una tabla de frecuencia muy extensa que aportaría muy poco valor a efectos de síntesis. (tal como se verá en la siguiente lección).
En este caso se agrupan los valores de la variable en intervalos de clase. El punto medio de cada intervalo de clase se denomina marca de clase y es el valor que representa la información contenida en el intervalo. Los extremos de los intervalos de clase se llaman límites de la clase. Las marcas de clase se calculan como el promedio de los límites superior e inferior de la clase. Las frecuencias absolutas de clase se obtienen contando el número de datos que caen en el intervalo correspondiente. A partir de estas se calculan las frecuencias absolutas acumuladas y las relativas, acumuladas o no, de clase. La tabla de frecuencias incorporarálosintervalos de clase,las correspondientes marcas de clase, y las frecuencias (absolutas y relativas, acumuladas o no) de clase.
La elección de los intervalos de clase, tanto en número como en amplitud (constante o variable), es una cuestión subjetiva del investigador, aunque hay una serie de procedimientos que podemos tener en cuenta:
- El número de intervalos K suele oscilar entre 5 y 20. Se puede determinar como K = √(n), con n como el número de datos. O también con la fórmula de Sturges: K = 1 + 3.3log(n) y en cualquier caso se aproxima el resultado al entero más cercano.
- La amplitud de cada intervalo suele ser fija y se calcula redondeando por exceso el cociente
| l = | R |
| −−− | |
| K |
- Los intervalos suelen elegirse semiabiertos por la derecha, esto es, de la forma [a, b), de tal manera que se solapen en los extremos, tomándose tantos cuantos sean necesarios para cubrir todo el recorrido de la variable. Observe que a ∈ [a, b), pero b ∉ [a, b).
En ocasiones los datos se presentan agrupados en intervalos no solapados. En tal caso es aconsejable (principalmente a efectos de su representación gráfica) reemplazarlos por otros del tipo anterior, cuidando de no modificar las frecuencias; esto se logra sustituyendo los extremos de los intervalos originales por los puntos medios de los extremos derecho e izquierdo de cada dos intervalos contiguos. Los nuevos extremos reciben el nombre de límites reales de clase.
Ejemplo. (Tomado de [1]. Convertir los siguientes intervalos de clase en intervalos con límites reales de clase. Hallar las marcas de clase. Elaborar la tabla de frecuencias.
| Intervalos | ni |
|---|---|
| 130 − 139 | 25 |
| 140 − 149 | 32 |
| 150 − 159 | 15 |
| 160 − 169 | 17 |
SOLUCIÓN
| Residente | Estatura | Residente | Estatura | Residente | Estatura |
| Residente1 | 1,15 | Residente 11 | 1,53 | Residente 21 | 1,21 |
| Residente 2 | 1,48 | Residente 12 | 1,16 | Residente 22 | 1,59 |
| Residente 3 | 1,57 | Residente 13 | 1,60 | Residente 23 | 1,86 |
| Residente 4 | 1,71 | Residente 14 | 1,81 | Residente 24 | 1,52 |
| Residente 5 | 1,92 | Residente 15 | 1,98 | Residente 25 | 1,48 |
| Residente 6 | 1,39 | Residente 16 | 1,20 | Residente 26 | 1,37 |
| Residente 7 | 1,40 | Residente 17 | 1,42 | Residente 27 | 1,16 |
| Residente 8 | 1,64 | Residente 18 | 1,45 | Residente 28 | 1,73 |
| Residente 9 | 1,77 | Residente 19 | 1,20 | Residente 29 | 1,62 |
| Residente 10 | 1,49 | Residente 20 | 1,98 | Residente 30 | 1,01 |
Si presentáramos esta información en una tabla de frecuencia obtendríamos una tabla de 30 líneas (una para cada valor -ya que son 30 residentes-), cada uno de ellos con una frecuencia absoluta de 1 y con una frecuencia relativa del 3,3% (de 1 / 30) ya que no hay una misma estatura para dos o mas personas. Esta tabla nos aportaría escasa información.
En lugar de ello, preferimos agrupar los datos por intervalos clases, con lo que la información queda más resumida (se pierde, por tanto, algo de información), pero es más manejable e informativa.
Si el analista decide tomar 10 clases de forma arbitraria sin aplicar la Formula de Sturges, esto da un ancho de clase de 0,9, y la construcción es como se ilustra en la siguiente tabla.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ahora, si se desea aplicar en primer lugar la Fórmula de Sturges y ser más riguroso en los cálculos y también apoyarse con Excel para que realice el conteo de los datos que están en cada intervalo de clase, de esta forma realizamos primero algunos cálculos básicos, con n = 30:
* Rango R = (Valor máximo) − (Valor mínimo) = 1,98 - 1,01 = 0,97
* K = 1 + 3,3*log(30) = 5,87 ≅ 6 Intervalos de clase (no redondee en el cálculo de l)
* l = R / K = 0,97/5,87 ≅ 0,165 ≅ 0,17
Como se tomaron los K intervalos de clase muy cerca al resultado de la fórmula, se debe ajustar el ancho de clase a 0,17 con lo cual se debe garantizar que con las clases se cubra completamente todos los datos. Se puede tomar la primera clase con el límite inferior un poco antes del valor mínimo de los datos, y asímismo que el límite superior de la última clase sea un poco superior al valor del dato máximo. Se organizan los datos en Excel en primer lugar en una columna y por facilidad y para verificación se organizan en orden ascendente. Luego se construyen los Intervalos de clase y se organiza la información como se observa en la siguiente figura:
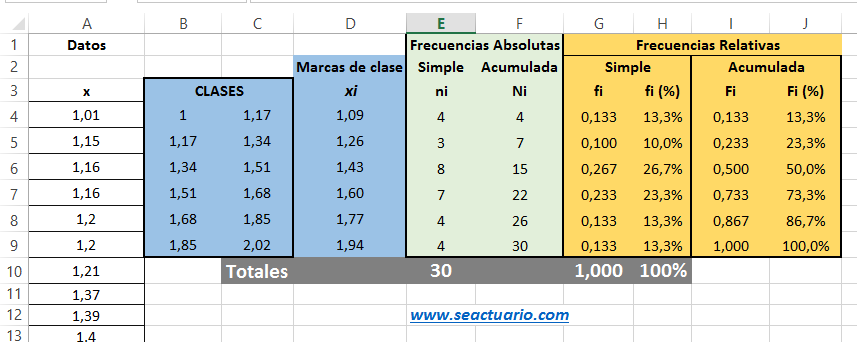
Por supuesto que la columna A tiene todos los datos hasta 1,98.
Con la función FRECUENCIA tome para los datos el rango de los mismos, y para grupos tome el limite superior de las clases hasta la penúltima, como se muestra en la figura:

Una vez se ingresa la fórmula en la primera celda, al presionar ENTER esta se propaga a todas las filas
Se muestran a continuación las fórmulas para que Excel realice el conteo de los datos (también se puede hacer manualmente contando ya que están los datos ordenados en la columna A)
| Celda | Fórmula |
|---|---|
| D4 | =CONTAR.SI($A$3:$A$32;">=1")-CONTAR.SI($A$3:$A$32;">=1,17") |
| E5 | =D5+E4 |
| F4 | =D4/$D$10 |
| H4 | =E4/$D$10 |
Observe como al construir los intervalos de clase, estos estrictamente deben ser con un intervalo cerrado en un extremo y abierto en el otro extremo, es decir, como (...] o como [...). Así en este ejemplo estos son de la forma:
[lim. inferior, lím. superior), de esta forma se debe garantizar que algún dato que
coincide con el el límite superior de la clase, no se vaya a contar dos veces. Por esta razón en la fórmula de la celda D4 se cuentan todos los datos superiores o iguales ( >= ) al lim.inf y se
le restan todos los datos mayores o iguales al lim.superior, es decir, se debe colocar la condición mayor o igual que (">=") en ambos extremos del Intervalo de Clase.
Una representación gráfica de los datos agrupados por intervalos de clase, corresponde a los histogramas, en que se grafican en barras con el ancho correpondiente a cada intervalo de clase, y con la altura correspondiente a la frecuencia absoluta
Puede descargar la Hoja de Excel Aquí.
En Excel, se puede obtener el Histograma con el complemento "Análisis de Datos", el cual se habilita en Archivo/Opciones y en la ventana emergente, seleccionar Complementos y luego hacer click en el botón Ir... para escoger los complementos de Excel que se desean instalar, como se observa en la figura:
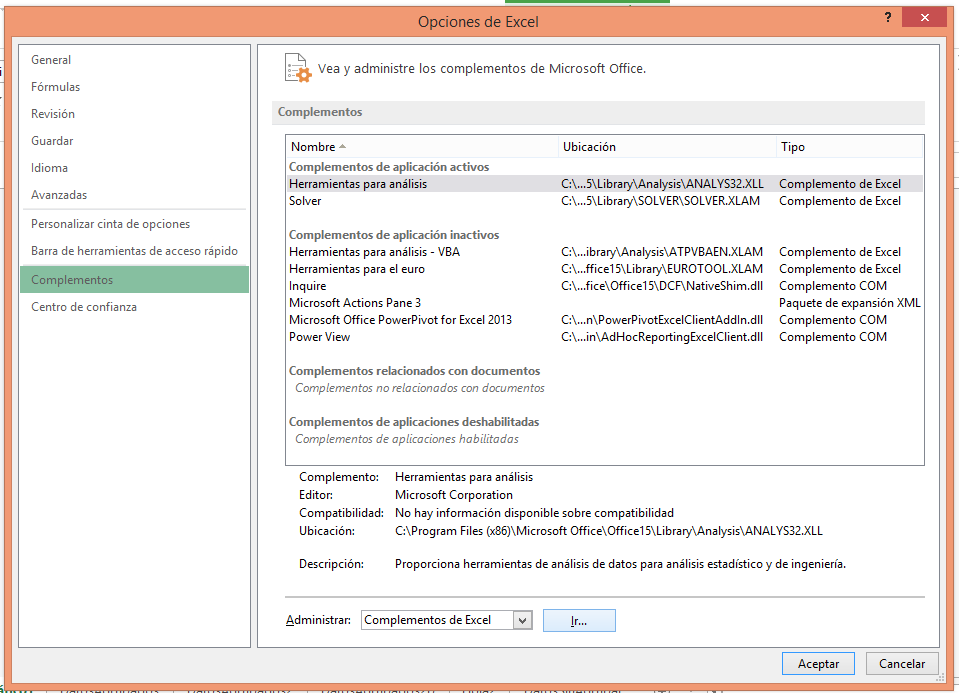
Luego se selecciona la opción Análisis de datos, como se observa en la siguiente figura y se presiona el botón Aceptar::
Luego de instalar el complemento, se hace click en la pestaña Datos y se observa en la parte superior derecha el complemento:

Ya instalado el complemento, dé click sobre éste y seleccione Histograma y luego presione Aceptar

En la ventana emergente, para Rango de entrada: seleccione los datos incluyendo la etiqueta del nombre, luego para Rango de clases: seleccione las clases que había copiado previamente (también puede permitir que Excel cree las clases), se deben chequar la opción Rótulos, en Rango de salida se escoge donde se desea que se generen las clases con sus frecuencias, aquí N4 (también se puede crear en otra hoja u otro libro), luego se chequea la opción Crear gráfico. Se puede observar en la siguiente figura esta configuración:
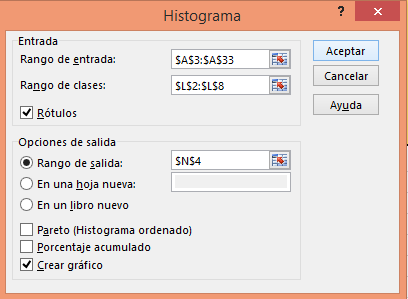
Excel genera la tabla de frecuencias y el gráfico del histograma como se observa:
 |  |
El gráfico se puede pasar a otra página y editarlo para una mejor presentación, por ejemplo como:
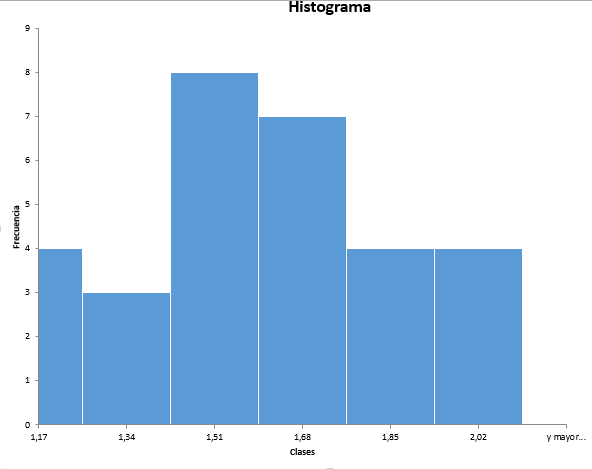
Ejmplo. Se tienen los pesos en kg-f de 50 estudiantes, como se muestra:
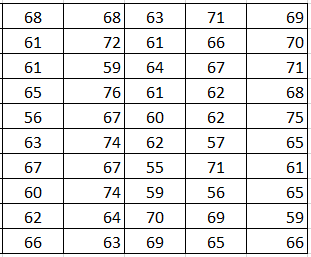
Realice la tabla con los datos agrupados y realice el histograma en Excel.
Solución. Al realizar un procedimiento similar al ejemplo anterior, se tiene:
- No. de clases con fórmula de Sturges: 6,6, se aproximan a 6
- Rango = 76 - 55 = 21
Ancho de clase = 21/6 = 3.5, se aproxima a 4 para trabajar con cantidades enteras.
Luego se toma el valor inicial del intervalo de clase No en 55 sino un poco antes, en 54.
De esta forma se obtiene la tabla de frecuencias para datos agrupados como:
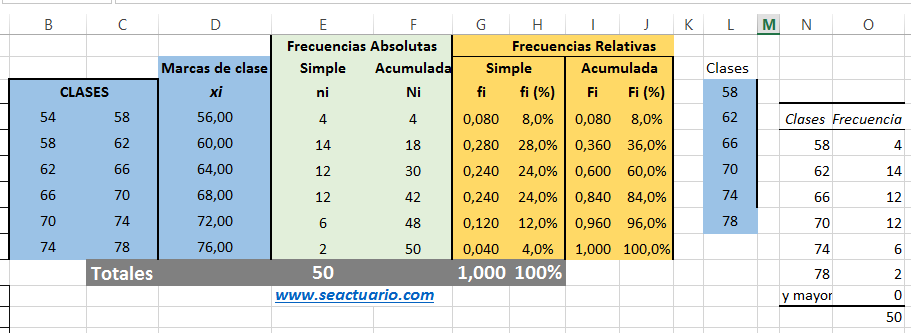
En este ejercicio y buscando que las frecuencias dadas para cada clase coincidan con los que arroja Excel, se cambia el intervalo con extremo izquierdo abierto y extremo derecho cerrado, es decr de la forma (...], por lo cual se cambia la fórmula en la celda E4, como
=CONTAR.SI($A$4:$A$53;">54")-CONTAR.SI($A$4:$A$53;">58")
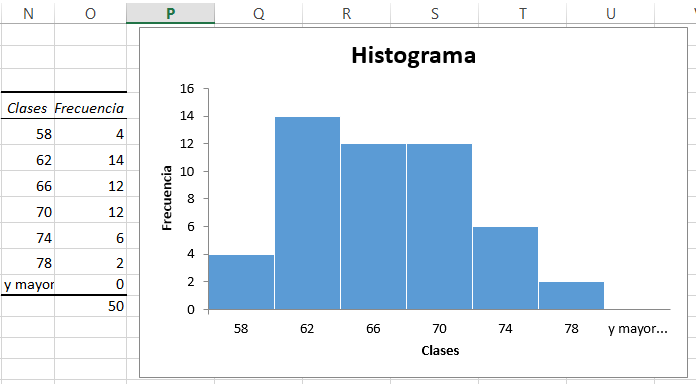
De la misma forma se corrigen las fórmulas de las siguientes celdas de la frecuencia absoluta. Al copiar los valores de la derecha de las clases para hacer el histograma, este arroja unas frecuencias absolutas que ahora sí coinciden con los obtenidos en la tabla, como se observa en la figura anterior, en las columnas N y O. El histograma con algún ajuste, es:
Ahora practique con Nuestro ejercicio Interactivo sobre tabla de frecuencias para datos agrupados
Puede descargar la Hoja de Excel con el formato de Datos Agrupados Aquí.
| Menú Probabilidad y Estadística | Anterior | Siguiente |