
 |
| Principal Cálculo | Anterior | Siguiente |
En los ejercicios siguientes, derivar la función (encontrar dy/dx).
| 1. |
 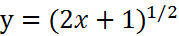  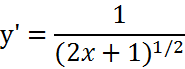 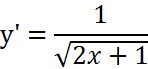
|
Recuerda que: 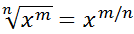 Ejemplo:  |
|
| 2. |
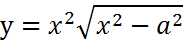  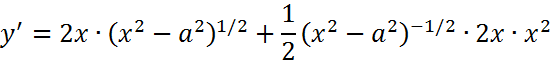 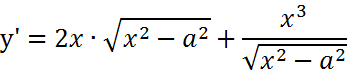 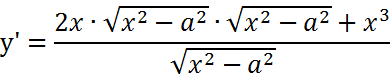 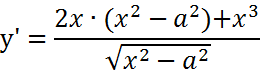 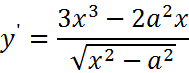 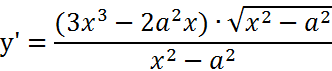
|
Expresamos la raíz como potencia: Ahora aplicamos las Reglas del Producto y la cadena: Volvemos a expresar como raíces y hacemos operaciones algebraicas: |
|
| 3. |
y =
2x + 1
/
2x − 1
y' =
2 ∙ (2x − 1) − 2 ∙ (2x + 1)
/
(2x − 1)2
y' =
4x − 4 − 4x − 4
/
(2x − 1)2
y' =
− 4
/
(2x − 1)2
|
Aplicando la derivada de un cociente, se tiene: Simplificando: |
|
| 4. |
y =
x2
/
1 − x2
y' =
2x∙(1 − x2) − x2∙(−2x)
/
(1 − x2)2
y' =
2x∙ − 2x3 + 2x3
/
(1 − x2)2
y' =
2x
/
(1 − x2)2
|
Aplicando la regla del cociente: Simplificando: |
|
| 5. |
y = sen2(1 + 3x) y = [sen(1 + 3x)]2 y' = 2∙sen(1 + 3x)∙cos(1 + 3x)∙(3) y' = 6∙sen(1 + 3x)∙cos(1 + 3x) |
Se aplica la regla de la cadena, y en esta la derivada del seno: |
|
| 6. |
y =
(2x2 + 5x)3/2
/
3
y =
1
/
3
∙(2x2 + 5x)3/2
y' =
1
/
3
∙
3
/
2
(2x2 + 5x)1/2 ∙(4x + 5)
y' =
1
/
2
∙ (4x + 5)∙ (2x2 + 5x)1/2
|
Como el denominador es constante, no es necesario aplicar la regla del cociente Aplicando la regla de la cadena: Simplificando: |
|
| 7. |
  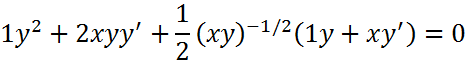 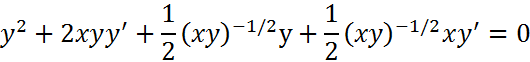 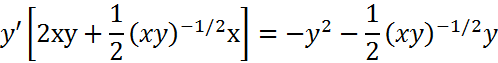  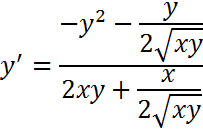 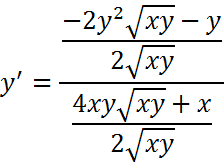  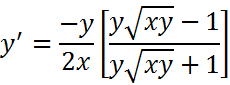
|
Expresamos raíces como potencias: aplicamos la regla de la cadena: Tenga en cuenta que al derivar y se debe agregar y' Se realizan los procedimientos algebraicos: Agrupamos y factorizamos y': Despejamos y' y reorganizamos volviendo a la forma de raíces: Simplificamos y reorganizamos la solución final |
|
| 8. |
x2 − y2 = xy 2x − 2y∙y' = 1y + x∙y' − 2y∙y' − x∙y'= y − 2x 2y∙y' + x∙y'= 2x − y y'∙[2y + x]= 2x − y y' =
2x − y
/
x + 2y
|
Derivando implícitamente: Agrupando las y': Multiplicando por −1: Se factoriza y': Se despeja y' y eso es todo. |
|
| Principal Cálculo | Anterior | Siguiente |