
| Menú Matemáticas Financieras | Anterior: Introducción a la Ingeniería Económica | Siguiente: El Interés Simple |
|---|
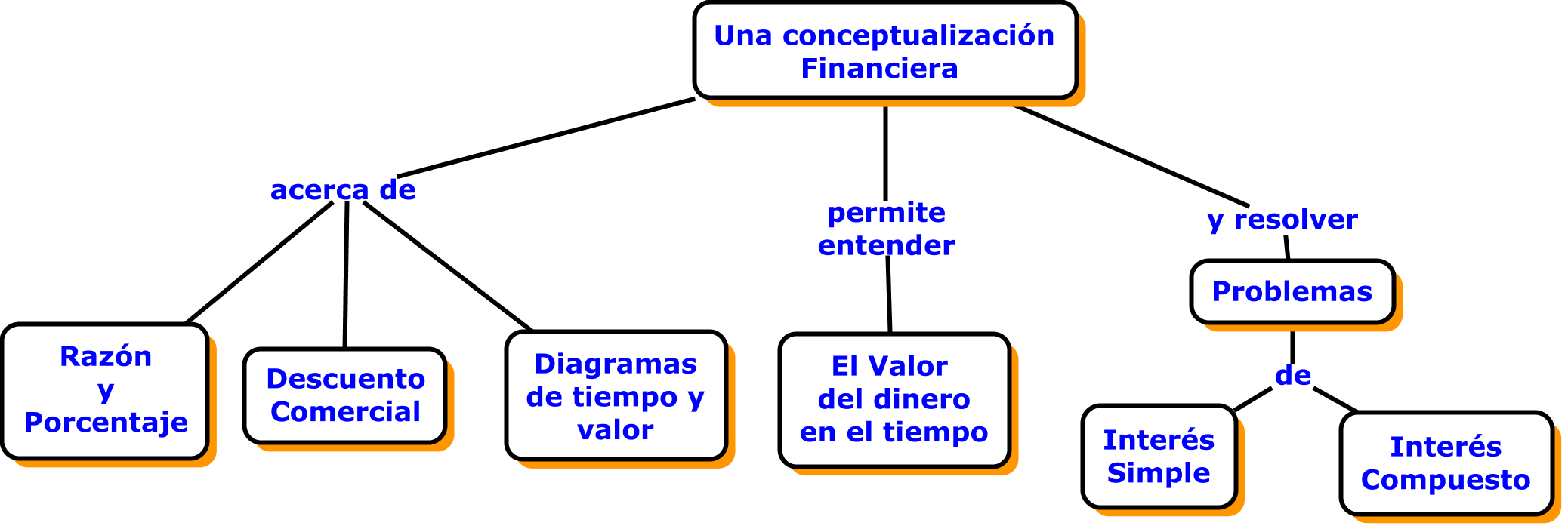
En este capítulo se expondrán definiciones y conceptos básicos de las Matemáticas Financieras y se hará precisión en el manejo de fórmulas y símbolos que se van
a utilizar en las diferentes temáticas a lo largo del curso. Además se realizarán algunos desarrollos en operaciones comerciales y financieras básicas. se van a tratar los temas de:
− Razón y Porcentaje.
− Descuento comercial.
− Diagramas de tiempo y valor.
− Valor del dinero en el tiempo.
− Interés –conceptos y tipos–.

Al finalizar el estudio del presente capítulo, el estudiante estará en capacidad de:
− Identificar y apropiar códigos del lenguaje financiero que le permitan comprender y aplicar operaciones de interés y descuento con apoyo de
conceptos matemáticos.
− Interpretar y explicar los alcances de las operaciones comerciales por medio de la elaboración de diagramas de tiempo y valor.
− Valorar el papel del gestor financiero en escenarios profesionales.
− Relacionar las causas y efectos de las decisiones financieras en los contextos empresariales, con base en postulados universales del Valor del
Dinero en el Tiempo.
La razón es el resultado de comparar dos cantidades o números. Por consiguiente, se pueden dar dos formas de comparación:
Consiste en cuánto excede una cantidad a otra. Por ejemplo 900 excede a 700 en 200
900 − 700 = 200Ej. La empresa A obtuvo utilidades en el mes de enero por 500 millones de pesos, la empresa B que es competidora de A, obtuvo a la vez 650 millones e pesos. Luego B excedió a las utilidades de su competidor A en
650 − 500 = 150 millones de pesosCompara dos cantidades dividiéndolas. Por ejemplo, la razón entre los sueldos del jefe y Pedro es de:
que se puede interpretar como que el Jefe gana 4 veces lo que gana Pedro.
La razón geométrica se puede expresar como:
− Fracción de la forma P/T: |
1/4 |
3/5 |
12/3 |
− Decimal: |
0.25 | 0.6 | 4 | − Porcentaje (%): |
25 % | 60 % | 400 % |
Se debe ser muy cuidadoso al expresar una razón en forma de porcentaje o viceversa, por ejemplo, 5% se divide entre 100 y equivale a 0.05
La Razón (R) se puede expresar como la Parte (P) sobre el Total (T), y al expresar como porcentaje, se interpreta precisamente como por cada 100 unidades del Total, nos da las unidades de la parte Parcial.
|
R =
P/T |
Así por ejemplo, si Pedro gasta $600.000 de su sueldo que es de $3.000.000, entonces podemos decir que:
| 600.000/3.000.000 = 0.2 = 20%
|
es decir, Pedro gasta el 20% de su sueldo en pagar el arriendo.
Ahora Pedro hace sus balances porque necesita ahorrar en los próximos dos años para los estudios universitarios de su hija.Sus gastos en pesos ($)son:
− Arriendo: 600.000
− Alimentación 400.000
− Servicios públicos: 300.000
− Cuota Tarjetas de Crédito: 250.000
− Cuota del Carro: 500.000
− Recreación: 300.000
− Pensión colegio: 200.000
Luego Pedro, manteniendo este nivel de gastos podría ahorrar $500.000, con lo que se tiene en términos porcentuales:
− Arriendo |
600.000/3.000.000 = 0.2 = 20.0% |
|---|---|
− Alimentación: |
400.000/3.000.000 = 0.133 = 13.3% |
− Servicios públicos: |
300.000/3.000.000 = 0.100 = 10.0% |
− Cuota Tarjetas de Crédito: |
250.000/3.000.000 = 0.083 = 8.3% |
− Cuota del Carro: |
500.000/3.000.000 = 0.1667 = 16.7% |
− Recreación: |
300.000/3.000.000 = 0.10 = 10.0% |
− Pensión Colegio: |
150.000/3.000.000 = 0.05 = 5.0% |
Ahora, se puede representar toda la distribución de los gastos y el ahorro de Pedro, como se observa en la siguente tabla:
| Ítem | Monto | Razón | |
|---|---|---|---|
| Decimal | Porcentaje | ||
| Arriendo | $600.000 | 0.20 | 20.0% |
| Alimentación | $400.000 | 0.133 | 13.3% |
| Servicios públicos | $300.000 | 0.10 | 10% |
| Cuota Tarjetas de Crédito | $250.000 | 0.083 | 8.3% |
| Cuota del Carro | $500.000 | 0.167 | 16.7% |
| Recreación: | $300.000 | 0.10 | 10% |
| Pensión Colegio: | $150.000 | 0.050 | 5.0% |
| Ahorro: | $500.000 | 0.167 | 16.7% |
| TOTAL (Sumas): | $3'000.000 | 1.0 | 100.0% |
Un grupo de amigos deciden invertir en un negocio prometedor de alta tecnología, las siguientes sumas de dinero: Sr. Andrés (A): $52.200.000; Señora Berta (B): $104.400.000, señor Carlos (C): $78.300.000 y señorita Daniela (D): $26.100.000. Al final del primer mes se obtiene una utilidad de $10.000.000. ¿Cómo se debe repartir esta utilidad?
En primer lugar se establece el total de los aportes realizados por los cuatro socios y sus porcentajes de participación en el negocio, de acuerdo a la fórmula:
Luego al elaborar la tabla con la distribución de las participaciones de los socios, se tiene:
| Socio | Aporte | Participación |
|---|---|---|
| A B C D | $52.200.000 $104.400.000 $78.300.000 $26.100.000 | 20% 40% 30% 10% |
| Total | $261.000.000 | 100% |
Luego asimismo se deben repartir las utilidades de $10.000.000, de acuerdo a la participación de cada socio, es decir, según sus aportes al total del negocio, con lo cual se obtienen estas ganancias de cada socio en la siguiente tabla:
| Socio | Participación | Utilidades |
|---|---|---|
| A B C D | 20% 40% 30% 10% | $2.000.000 $4.000.000 $3.000.000 $1.000.000 |
| Total | 100% | $10.000.000 |
El manejo adecuado de los conceptos matemáticos básicos abordados anteriormente, permite el avance frente a la profundización de los temas centrales de la asignatura, entre los cuales se encuentran: descuento, interés, tasas equivalentes, etc.
Precio de lista: Es la cantidad que se cotiza en el catálogo de una empresa. El precio que se recomienda vender un producto antes de conceder un descuento.
El Descuento Comercial es una reducción del precio de lista de un bien o servicio. Dicha reducción se expresa normalmente en términos porcentuales. Estos descuentos se suelen conceder a los clientes finales de los productos con fines de promoción, o a los intermediarios en el canal de distribución por pronto pago, entre otras razones.
Ejemplo 3. ¿Cuál es el precio de venta de una Máquina cuyo precio de lista es $60.000.000 y se promete un descuento del 6% por pago de contado? ¿A cuánto dinero equivale el descuento?
Hay dos preguntas por resolver. Inicialmente se establece a cuánto dinero equivale el descuento.
| Precio de lista | tasa de descuento | Descuento | ||
| $ 60.000.000 | * | 0.06 | = | $ 3.600.000 |
El descuento es de $3.600.000. Ahora se toma el precio de lista y se resta el descuento para establecer el precio de venta:
| Precio de lista | Descuento | Precio de Venta | ||
| $ 60.000.000 | − | $ 3.600.000 | = | $ 56.400.000 |
Solución: El precio de venta fue de $ 56.400.000 y el descuento fue de $ 3.600.000
Ejemplo 4. Un carro cuyo precio original era de $ 45.000.000 finalmente fue vendido por $ 40.500.000. ¿De cuánto fue la tasa de descuento aplicada?
Solución: Para establecer el descuento en pesos, simplemente se halla la diferencia entre el precio de lista y el precio de venta:
| Precio de lista | Precio de venta | Descuento | ||
| $ 45.000.000 | − | $ 40.500.000 | = | $ 4.500.000 |
Luego, mediante la fórmula ya trabajada y con respecto a los términos de la fracción, en este caso la parte P = D, donde D es el descuento obtenido, y el total T = Precio de Lista, así se establece la tasa de descuento aplicada:
D/Precio Lista = |
4.500.000/45.000.000 = 0.10 = 10% |
Respuesta: El descuento fue de $ 4.500.000 que corresponde al 10% del precio de lista
Ejemplo 3. Jaime compró una motocicleta y pagó $ 5.980.000 una vez aplicado el descuento del 8% por haberla comprado en un día libre del Impuesto a las Ventas que decretó el gobierno nacional. ¿Cuál es el valor de lista de la motocicleta?
En este caso no se sabe el precio de lista, tampoco se sabe la cantidad de descuento aplicado pero sí se conoce la tasa y el valor de la motocicleta con el descuento aplicado, luego con la fórmula, llamando D al descuento según D = Precio de Lista − Precio de Venta:
D/Precio de Lista = |
(Precio de Lista) − 5.980.000 /Precio de Lista = 0.08 |
Al despejar se tiene:
(Precio de Lista) − 5.980.000 = 0.08*(Precio de Lista)
(Precio de Lista) − 0.08*(Precio de Lista) = 5.980.000
0.92*(Precio de Lista) = 5.980.000
| (Precio de Lista) = 5.980.000/0.92 = $ 6.500.000 |
Respuesta: El valor de lista de la motocicleta es de $ 6.500.000
Observaciones: Si la tasa de descuento es del 8%, esto implica que se paga el 92% del valor del artículo. Es común el error de tomar la base o Total sobre el precio ya con el descuento, luego se debe ser cuidadoso en tener presente que en este caso el Total no se conoce.
En el apartado anterior se abordaron operaciones que se realizan en un solo momento del tiempo. Se entrará ahora, a analizar algunas transacciones que requieren una mirada progresiva en el tiempo, para lo cual es conveniente reconocer herramientas que faciliten una mejor comprensión del Valor del Dinero en el Tiempo.
En este tema se manejarán las siguientes convenciones:
1. La flecha horizontal representa el tiempo. El tiempo fluye hacia la derecha desde el Presente hasta un momento Futuro. En esta flecha se escribirán las fechas o los períodos de las transacciones.
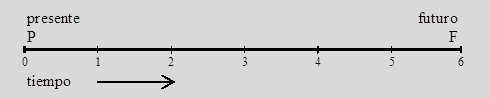
2. Las flechas que si dirigen hacia arriba o hacia abajo son valores monetarios, es decir, representan dinero. Se ha convenido que las flechas hacia arriba representan ingresos y hacia abajo representan egresos.
Por ejemplo, si se realiza una inversión de $500.000 y dentro de 6 meses se reciben $600.000, entonces el diagrama de tiempo y valor será:
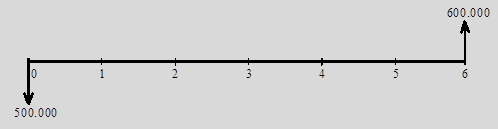
Ejemplo 5
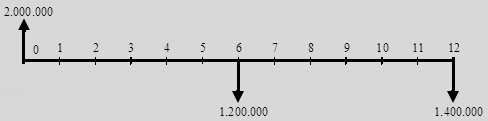
El Fondo de Empleados realiza un préstamo por valor de $2.000.000 y recibe dos pagos así: $1.200.000 dentro de 6 meses y $1.400.000 dentro de 12 meses. Se representan estas operaciones financieras mediante un Diagrama de Tiempo y Valor. En este caso es posible hacer la representación gráfica desde dos puntos de vista: Desde el Fondo de Empleados o desde el Empleado. Para el Fondo de Empleados (Prestamista): los $2.000.000 constituyen un desembolso, el cual se representa con una flecha hacia abajo; y las cuotas que recibe constituyen ingresos, que se representan con flechas hacia arriba, así:
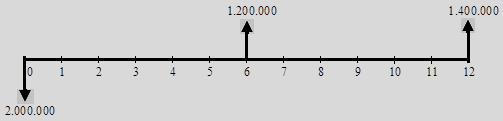
Ahora vemos que el diagrama de Flujo de Caja es relativo o depende del punto de vista de quien lo realice, en este caso para el Empleado (Deudor), la representación gráfica es inversa. Los $2.000.000 constituyen un ingreso, que se representa con una flecha hacia arriba y las cuotas que paga constituyen egresos, los cuales se representan con flechas hacia abajo, así:
Documento mercantil en el que está incorporado un derecho privado patrimonial. Es también un documento de contenido crediticio en el que se incorpora un derecho literal y autónomo de cobro o de pago de un activo o de un valor, los cuales normalmente son transmisibles ya que pasan de unas personas a otras. Algunos títulos valores comunes son el Cheque, La Letra de Cambio y el Pagaré.
El dinero adquiere un valor que depende del tiempo. Esto significa que la cuantía consignada en un billete o en un título valor sufre variaciones en relación con su poder adquisitivo, conforme transcurre el tiempo. Este fenómeno se produce debido a las alteraciones de los precios de los bienes y servicios en una economía
Así, diez millones de pesos de hoy tienen un valor diferente a diez millones de pesos ubicados hace cinco años (pasado) y que los diez millones de pesos ubicados dentro de cinco años (futuro). Esto se debe a fenómenos como la pérdida del poder adquisitivo del dinero o Inflación, y a llos intereses o rendimiento que debe generar un capital.
Observe el Diagrama de Tiempo y Valor que ilustra esta afirmación:
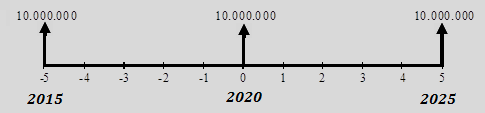
Las distancias de estas cifras en el tiempo hacen que no exista una equivalencia entre ellas en cuanto a su capacidad de pago. En el pasado era posible adquirir mayor cantidad de bienes y servicios con cierta cantidad de dinero, comparado con los que se podrían adquirir hoy o en el futuro, con la misma cantidad.
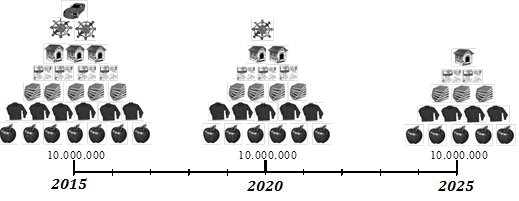
Por esta razón, se puede afirmar que las cantidades de la Gráfica 1.6 NO son equivalentes, por cuanto NO es indiferente la selección entre cual-quiera de ellas. Por el contrario, se prefiere el dinero ubicado en el pasado por su capacidad de adquirir mayor cantidad de bienes y servicios.
Observación: En las transacciones comerciales y financieras se da por supuesto que al invertir cierta cantidad de dinero, esta debe producir un rendimiento que depende del tiempo y de la tasa de interés pactada. Si invertimos un capital, y verificamos su valor en el futuro, este habrá aumentado por efecto de la acumulación de los rendimientos que ha generado. En el mercado real, se debe considerar también el riesgo, y tener en cuenta que a mayor tasa de interés también se incrementa el riesgo. Entre dos cantidades de dinero de igual valor nominal, se ha de preferir la que esté ubicada hoy, a una que esté ubicada en el futuro, debido a que es posible invertir esa cantidad de hoy para que en el futuro haya generado unos rendimientos.
Es de resaltar que No es posible asociar cantidades de dinero que se encuentren en diferentes posiciones en el tiempo. Para poder hacerlo, es necesario trasladar esas cantidades utilizando ecuaciones que permitan reflejar el verdadero Valor del Dinero en el Tiempo, es decir, para poder comparar cantidades en diferentes puntos en la línea del tiempo, hay ecuaciones para trasladar todas las cantidades monetarias a un mismo punto en la línea del tiempo. Esta, es precisamente la intención de los siguientes temas, que se ocupan de establecer algunos tipos de equivalencias.
| Menú Matemáticas Financieras | Anterior: Introducción a la Ingeniería Económica | Siguiente: El Interés Simple |
|---|