
| Principal Cálculo | Anterior | ... |
Las integrales impropias son fundamentales en áreas como la Probabilidad. En la siguiente figura se observa la forma de la distribución normal, la cual tiene la forma acampanada. La región se extiende infinitamente a ambos lados, sin embargo el área total es finita.
 |
∘ este tipo de funciones que no están limitadas, se pueden representar apropiadamente con las integrales impropias. En este tipo de integrales, uno o ambos de los límites pueden ser infinitos, como:
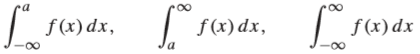 |
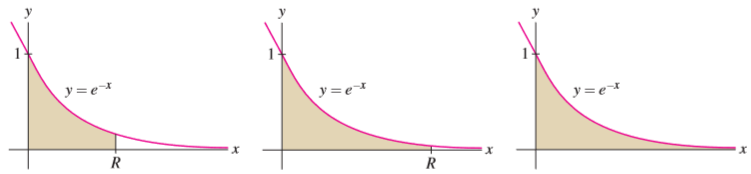
¿Cómo calcular el área de una región no limitada (también se dice No acotada), y por qué esta es finita? Veamos un ejemplo tomado de [1 calculus]. Considere el Area (fig. 2A) bajo la curva de f(x) = e-xAh sobre el intervalo finito [0, R]:
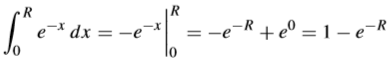
Como R → ∞, esta área se aproxima a un valor finito (fig. 2B):
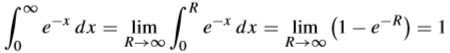
Parece razonable tomar este límite como la definición del área bajo la curva (o la grafica o la función) en el intervalo infinito [0, ∞). Así la región No acotada de la fig. 2C tiene área 1.
 |
||
| Fig. 2A La región finita tiene área 1 − e-x | Fig. 2B El área se aproxima a 1 como R → ∞ |
Fig. 2C La región no acotada tiene area 1 |
|
Ejercicios. Demuestre el resultado de las siguientes integrales
Ejercicios: Resuelva las siguientes integrales
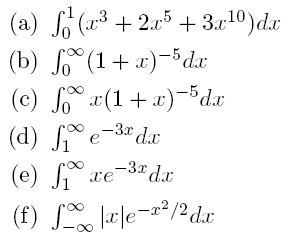 |

| Principal Cálculo | Anterior | ... |