Cálculo ejercicios resueltos de integrales por sustitucion

Integración Sustitución

Para encontrar: ∫ f(x)dx sustituya u= g(x), con g que sea diferenciable, luego derive: du =g′(x)dx

Entonces se puede escribir ∫ f(x)dxcomo una integral con respect a la variable u.

De esta forma, esto cambia la integral original
∫ f(x)dx a una integral como ∫ h(u)du y con H como la antiderivada de h(u)du, entonces

Ejemplo. Integre : ∫(x³ − 1)^4/3x²dx	⇒ Substitución: u = x³ − 1 Así que du = 3x²dx → ⅓du = x²dx
Ahora la integral se puede escribir como
∫u^4/3⅓du = ⅓∫u^4/3du
Ahora se sustituye hacia atrás u = x³ − 1 que da como resultado final

1. Integrar la función:	Sustitución:	Consulte con frecuencia seactuario.com, estamos renovando y publicando nuevo material educativo todos los dias *Comprobación...*

Resuelva la integral indefinida: 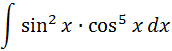Se reescribe el cos⁵x como: 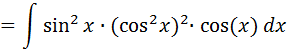Luego por identidad trigonométrica se tiene: 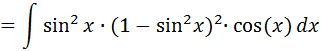Se aplica ahora la sustitución: 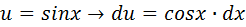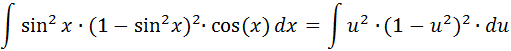Desarrollando el binomio al cuadrado y luego resolviendo el factor: 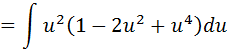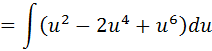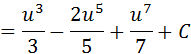Ahora volvemos a la variable original, y se tiene resuelta la integral:	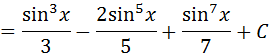	*Comprobación...*


		*Comprobación...*

		*Comprobación...*